Development of an online project
by Valentin Chelnokov
The name of my project Dagaz was inspired by the name of the twenty-third Elder Futhark rune ᛞ, which can be translated as “revival.” This rune reminds me of a board game piece and its meaning corresponds to the idea of stimulating interest in abstract games through the creation of a universal game engine both for players and designers.
My passion for board games started with two events. First of all, I met Dmitry Skiryuk—Russian writer and a great enthusiast of games such as Go, Checkers, and the Mancala family of games (mainly the African branch of them). At about the same time I discovered the Zillions of Games game engine. Unfortunately, I got acquainted with this project quite late, when the main excitement around it had already begun to wane. But it did not stop me from making several dozen games and writing a large number of articles on this topic. The Zillions Rules File scripting language (called the “ZRF” meta-language for short) literally turned my mind upside down. I could not imagine how many completely different games could be created with it.
The further I progressed in the study of ZRF, the more I realized that only fairly simple games, preferably similar to Checkers or Chess, were easily implemented in it. When it came to something more complicated, such as Mancala, for example, I had to use bulky and obscure structures that worked slowly and unreliably. And so, I mastered the Axiom Development Kit, a plug-in DLL extension for Zillions developed by Greg Schmidt. This allowed me to develop more complex games, such as Rithmomachia (see also AG15), but it was still difficult and time consuming. Besides that, both Axiom and Zillions only worked with Windows, but I wanted to see a cross-platform solution that could be run anywhere, even on a smartphone.
Demand for such a solution determined the choice of technology. The only programming language natively supported by almost all modern Internet browsers is JavaScript. I did not want to handle Java applets, which are already considered outdated and inconvenient technology. The WebAssembly technology, in turn, was not suitable for me, for some other reasons. My goal was to make every user able to have full access to the open-source code of a program while it runs, so users could figure it out and develop their own games in the same way as they can in Zillions of Games, but more easily.
Of course, any approach has its drawbacks. The downside of JavaScript's openness is its relatively low performance, compared to computer languages such as C++ or Java. After a series of failed experiments, I realized that I would not be able to interpret the ZRF description directly while running the game. It worked too slowly. Then I created Z2J, which converts ZRF files into JavaScript code. The converted game description code looks too machine-generated and is difficult to edit manually, but it is as understandable as ZRF.
My passion for board games started with two events. First of all, I met Dmitry Skiryuk—Russian writer and a great enthusiast of games such as Go, Checkers, and the Mancala family of games (mainly the African branch of them). At about the same time I discovered the Zillions of Games game engine. Unfortunately, I got acquainted with this project quite late, when the main excitement around it had already begun to wane. But it did not stop me from making several dozen games and writing a large number of articles on this topic. The Zillions Rules File scripting language (called the “ZRF” meta-language for short) literally turned my mind upside down. I could not imagine how many completely different games could be created with it.
The further I progressed in the study of ZRF, the more I realized that only fairly simple games, preferably similar to Checkers or Chess, were easily implemented in it. When it came to something more complicated, such as Mancala, for example, I had to use bulky and obscure structures that worked slowly and unreliably. And so, I mastered the Axiom Development Kit, a plug-in DLL extension for Zillions developed by Greg Schmidt. This allowed me to develop more complex games, such as Rithmomachia (see also AG15), but it was still difficult and time consuming. Besides that, both Axiom and Zillions only worked with Windows, but I wanted to see a cross-platform solution that could be run anywhere, even on a smartphone.
Demand for such a solution determined the choice of technology. The only programming language natively supported by almost all modern Internet browsers is JavaScript. I did not want to handle Java applets, which are already considered outdated and inconvenient technology. The WebAssembly technology, in turn, was not suitable for me, for some other reasons. My goal was to make every user able to have full access to the open-source code of a program while it runs, so users could figure it out and develop their own games in the same way as they can in Zillions of Games, but more easily.
Of course, any approach has its drawbacks. The downside of JavaScript's openness is its relatively low performance, compared to computer languages such as C++ or Java. After a series of failed experiments, I realized that I would not be able to interpret the ZRF description directly while running the game. It worked too slowly. Then I created Z2J, which converts ZRF files into JavaScript code. The converted game description code looks too machine-generated and is difficult to edit manually, but it is as understandable as ZRF.
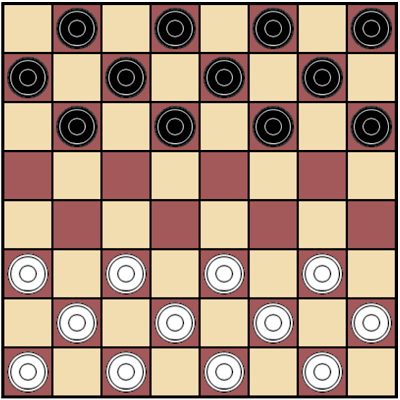
I started with Russian Checkers, with the rules here, because I always considered the games of this family greatly undervalued. Without understanding its complex game mechanics all further development would be meaningless. Particularly, I am talking about composite moves. The fact that a move can consist of several consecutive moves is a very important matter. Another contribution of Checkers is the implementation of priority moves. If there is an opportunity to capture an enemy piece, it must be captured. Capturing is compulsory even if in future it weakens the player's position. Subsequently, the priority moves mechanism had to be entirely reconsidered and updated for many other games, but it firmly formed the foundation of the Dagaz project.
Chess pitched me the idea that some moves can consist of multiple pieces moving at once (e.g., castling). Moreover, not all possible piece moves can be allowed--the King for example may never move himself into check, where he could be captured. So I had to implement a verification mechanism for a checkmate. Checkmate verification (move prohibition) is more difficult than priority capturing in Checkers, since the prohibition can apply to any moves, both “capturing” and “non-capturing.” Checkers can also have different verification rules, being far from simple. In some types of games, it is necessary to capture the maximum possible number of enemy pieces, and other games, such as Frisian Checkers (see also AG10) , go even further, giving priority to capture crowned (promoted) pieces first.
I could not afford to waste time describing such a complex problem in the logic of ZRF checks and then translate it into JavaScript, even if I knew how to do it. Anyway, the code obtained from Z2J in this way is not very optimal. It is much more reasonable to describe such verifications in JavaScript directly. I used ZRF just to describe the basic logic for moving pieces, but passed rules verification to JavaScript-extensions. Before entering the UI, the list of moves generated by the game's preset is passed to additional modules connected to the game. The extension module can effectively perform complex checks, prohibit individual moves, and enrich them by additional actions.
Chess pitched me the idea that some moves can consist of multiple pieces moving at once (e.g., castling). Moreover, not all possible piece moves can be allowed--the King for example may never move himself into check, where he could be captured. So I had to implement a verification mechanism for a checkmate. Checkmate verification (move prohibition) is more difficult than priority capturing in Checkers, since the prohibition can apply to any moves, both “capturing” and “non-capturing.” Checkers can also have different verification rules, being far from simple. In some types of games, it is necessary to capture the maximum possible number of enemy pieces, and other games, such as Frisian Checkers (see also AG10) , go even further, giving priority to capture crowned (promoted) pieces first.
I could not afford to waste time describing such a complex problem in the logic of ZRF checks and then translate it into JavaScript, even if I knew how to do it. Anyway, the code obtained from Z2J in this way is not very optimal. It is much more reasonable to describe such verifications in JavaScript directly. I used ZRF just to describe the basic logic for moving pieces, but passed rules verification to JavaScript-extensions. Before entering the UI, the list of moves generated by the game's preset is passed to additional modules connected to the game. The extension module can effectively perform complex checks, prohibit individual moves, and enrich them by additional actions.
Atari Go, with the rules here, perfectly illustrates what has been said above. Standard moves in this game are pretty simple—just place a stone on any vacant intersection (“point” of the board). But not all kinds of moves are allowed—a “suicide” move that makes a player lose the last liberty of his group of stones is forbidden. A player may not place a stone such that it or its group (called “chain”) immediately has no liberties (i.e., vacant points adjacent to a stone, along one of the grid lines of the board), and a chain of stones must have at least one liberty to remain on the board. At the same time, it is checked if a player's move surrounds the opposing stones so that they have no liberties—then those opposing chains are captured and removed from the board (if happening in Atari Go, it means losing the game). All these checks and verifications are too difficult and numerous to be done in ZRF.
When I was experimenting with Zillions of Games, I discovered another problem related to the game of Go. When removing a large number of stones at once (this situation is rare, but still possible), the application crashes, as a result of an overflow of the internal memory buffer. Zillions saves each move and all changes that occur after in text format (ZSG notation). Move description consists not only of the action of placing a stone by itself but also all other attributes attached to the stone and its neighbours: including player, position, piece removals, etc. But since captures in Go are completely determined by adding only one stone to the current position, it should be enough just to verify that a stone was placed. In Dagaz, captures with removals in games such as Go or Checkers are considered as side effects that directly follow from the rules of the game when making a move. The program core, in accordance with the rules, can always restore all of the changes and side effects and automatically adjust them to the main sole action, so there is no need to include this information in the text description of every move. As a result, the description of the moves made is very brief and uncluttered.
One other question that Dagaz helps to solve is software rendering and positioning of a piece on the board. In Zillions, for each piece there is a limited number of bit flags, describing each piece's attributes in terms of “Yes = 1” and “No = 0.” For example, it is used in Chess castling—the King and the Rook that you would castle with must not have been moved earlier in the game. Any move of any of these pieces changes the value of a bit flag from No to Yes—“Was there a turn with a move preventing pieces from castling? Yes, there was. And no castling is allowed anymore.” Dagaz avoids the limits on value-type present in ZRF. It can save not only Boolean values, but any other kind of attribute and its value-type. Playing Mancala needs to use an integer number value-type to show the quantity of pieces (“seeds”) in each defined hole (“house”).
When I was experimenting with Zillions of Games, I discovered another problem related to the game of Go. When removing a large number of stones at once (this situation is rare, but still possible), the application crashes, as a result of an overflow of the internal memory buffer. Zillions saves each move and all changes that occur after in text format (ZSG notation). Move description consists not only of the action of placing a stone by itself but also all other attributes attached to the stone and its neighbours: including player, position, piece removals, etc. But since captures in Go are completely determined by adding only one stone to the current position, it should be enough just to verify that a stone was placed. In Dagaz, captures with removals in games such as Go or Checkers are considered as side effects that directly follow from the rules of the game when making a move. The program core, in accordance with the rules, can always restore all of the changes and side effects and automatically adjust them to the main sole action, so there is no need to include this information in the text description of every move. As a result, the description of the moves made is very brief and uncluttered.
One other question that Dagaz helps to solve is software rendering and positioning of a piece on the board. In Zillions, for each piece there is a limited number of bit flags, describing each piece's attributes in terms of “Yes = 1” and “No = 0.” For example, it is used in Chess castling—the King and the Rook that you would castle with must not have been moved earlier in the game. Any move of any of these pieces changes the value of a bit flag from No to Yes—“Was there a turn with a move preventing pieces from castling? Yes, there was. And no castling is allowed anymore.” Dagaz avoids the limits on value-type present in ZRF. It can save not only Boolean values, but any other kind of attribute and its value-type. Playing Mancala needs to use an integer number value-type to show the quantity of pieces (“seeds”) in each defined hole (“house”).
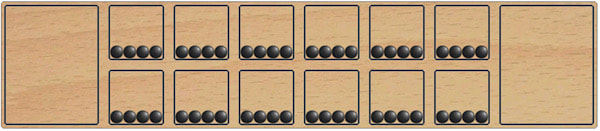
Oware, with the rules here, is the most famous of the African Mancala family of games. The game starts with four seeds in each house. Players take turns moving the seeds. On a turn, a player chooses one of the six houses under his control (except scoring houses at the sides—one for each player). The player takes all seeds from one house, and distributes them, dropping one in each house counterclockwise from the house he has chosen, in a process called "sowing." Seeds are not distributed into the end scoring houses, nor into the house drawn from. If the last seed is dropped in the opponent's house and its total quantity is 2 or 3 there, then all seeds are removed from this house and put in your scoring house. If the previous-to-last seed also brought an opponent's house to 2 or 3, these are captured as well, and so on. The object of the game is to capture more seeds than one's opponent and to store them in your scoring house.
It is not surprising that Zillions of Games meets several obstacles to implement the mechanics of Mancala. First of all, the piece image in this game is just a picture. Zillions cannot draw it with the help of a programming language, so no software rendering is possible. As a result, in each house different numbers of seeds had to be encoded as a separate type of piece, 1 seed is 1 piece and 2 seeds is not 2 pieces but is another type of piece entirely. This mechanic increases the number of images needed to describe the corresponding number of pieces in an arithmetic progression. It is still complicated by the lack of ability to work with integers, and you need to use bit flags to emulate normal addition and subtraction. In the Axiom Development Kit, integer arithmetic was added, but Mancala continued to be a tough nut to crack. In Dagaz, I went further along the path of simplifying the structural description of such games. As a bonus, simpler solutions tend to work more efficiently.
It is not surprising that Zillions of Games meets several obstacles to implement the mechanics of Mancala. First of all, the piece image in this game is just a picture. Zillions cannot draw it with the help of a programming language, so no software rendering is possible. As a result, in each house different numbers of seeds had to be encoded as a separate type of piece, 1 seed is 1 piece and 2 seeds is not 2 pieces but is another type of piece entirely. This mechanic increases the number of images needed to describe the corresponding number of pieces in an arithmetic progression. It is still complicated by the lack of ability to work with integers, and you need to use bit flags to emulate normal addition and subtraction. In the Axiom Development Kit, integer arithmetic was added, but Mancala continued to be a tough nut to crack. In Dagaz, I went further along the path of simplifying the structural description of such games. As a bonus, simpler solutions tend to work more efficiently.
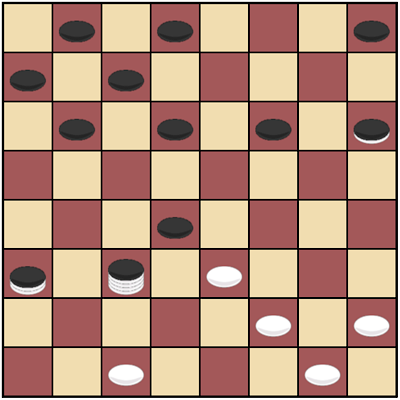
Russian Column Checkers, also known as Bashne (see AG1 and other issues) are very similar to Mancala games, but there is one exception. Unlike seeds put together in one house, the order of pieces in a column matters, not only their quantity. Integer numbers are not enough to describe the organization of a column with pieces placed in a specific order, so I added more types of values to the Dagaz attributes. To describe the order of pieces in a column, I use strings as attributes. Actually, Dagaz makes it possible to use arrays and even other data structures, but I prefer to use text, because it is easier to save in a file. Using software rendering to display each piece is a very powerful feature to control it. Here is an example of how this option can be used: in the game of Go there is a super-ko rule, which says that players are not allowed to make a move that returns the game to a previous position. For its visualization, a square is used, which is not a piece, but is simply displayed on the board as an image to mark a field that is not available for the player's move. In Renju (AG5 and AG6), the list of forbidden moves differs, but I also used the same software-rendered square to display them.
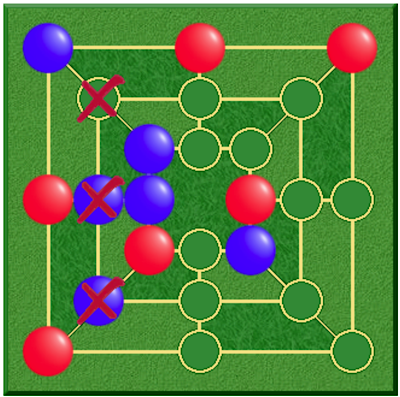
Rules prohibiting making a move that returns the game to the previous position can be fairly complicated. The aim of Morabaraba, with rules here, is to create a "mill" by placing a cow (piece) on an empty intersection on the board—a mill is a row of three cows on any line drawn on the board. If a player forms a mill, he may remove or "shoot" one of the opponent's cows. The shot cow is removed from the board and not placed again. A cow in a mill may not be shot unless all of the opponent's cows are in mills, in which case any cow may be shot. A mill which is broken to form a new mill cannot be formed again on the next move. Red crosses in Figure 6 mark the mill broken by the previous move. But, even when an intersection is crossed, the player still can place a cow there if this move will not rebuild the mill in this turn.
The same ability to display images on the board that are not related to pieces can be used for other purposes than prohibiting repeating positions. There are games where some of the information is hidden from the player. Usually, when we talk about games with hidden information, we mean card games, but the same principle applies to some chess-family games. In the game Dark Chess, the player does not see the spaces on the board that they cannot attack. The same idea can be applied to other chess-type games.
Dark Yonin Shogi, is a version of Yonin Shogi. Yonin Shogi is a famous Japanese game for four players. As with the other classical Shogi games which are played on small and middle size boards, Yonin Shogi saved the "drop rule," whereby captured pieces are retained in hand and can be brought back into play under the capturing player's control. On any turn, instead of moving a piece on the board, a player may select a piece in hand and place it on any empty square. Since there are four players, the game does not end after the first King is captured. All captured Kings as well as other pieces are sent to the hand reserve, and the player left without a King cannot move his pieces. Yonin Shogi can be played “in the dark” also—as in Dark Chess, Dark Yonin Shogi uses the concept "fog of war," which hides the part of the board that is outside of the player's attacks.
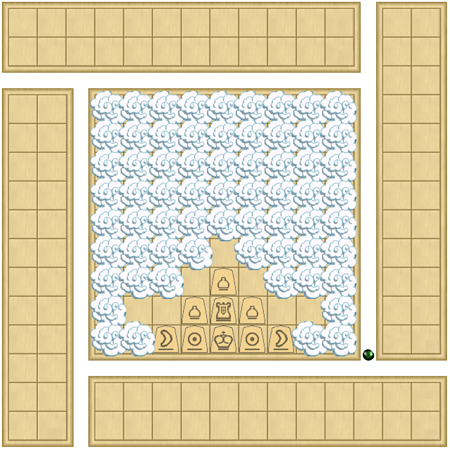
Developing these “dark” games’ mechanical peculiarity, Dagaz can use two special features for hiding both empty cells and even cells containing pieces—pieces can be made translucent, and if needed cells whether they are empty or not can be additionally hidden by an image covering them like an upper layer. The display of individual pieces is controlled by checking whether they are attacked or not. If the opponent's piece is not attacked, it is not shown, and the same check is performed for the player’s own pieces—the player's pieces that are not under attack are displayed as translucent. In principle, this verification would be enough to hide pieces in the game. However, it does not make it obvious whether a cell is empty or contains a translucent enemy piece. For this reason, a user asked me also to mark empty fields that are not under attack. This is how “clouds” appeared in the game (see Figure 7). The "cloud” is a software rendered image to show a cell is out of attack range. The player now keeps in mind that there is still a possibility that a cell can contain a translucent enemy piece, and he does not know if a cell is empty or not. However, it is obvious that an uncovered cell with no “cloud” and no visible piece inside it is just empty.
Developing these “dark” games’ mechanical peculiarity, Dagaz can use two special features for hiding both empty cells and even cells containing pieces—pieces can be made translucent, and if needed cells whether they are empty or not can be additionally hidden by an image covering them like an upper layer. The display of individual pieces is controlled by checking whether they are attacked or not. If the opponent's piece is not attacked, it is not shown, and the same check is performed for the player’s own pieces—the player's pieces that are not under attack are displayed as translucent. In principle, this verification would be enough to hide pieces in the game. However, it does not make it obvious whether a cell is empty or contains a translucent enemy piece. For this reason, a user asked me also to mark empty fields that are not under attack. This is how “clouds” appeared in the game (see Figure 7). The "cloud” is a software rendered image to show a cell is out of attack range. The player now keeps in mind that there is still a possibility that a cell can contain a translucent enemy piece, and he does not know if a cell is empty or not. However, it is obvious that an uncovered cell with no “cloud” and no visible piece inside it is just empty.
Such radical modifications are not always concerned with improving the appearance of a game. In some games, such as Gala (also known as Farmer's Chess), pieces may change direction during their move. In Indonesia's Surakarta (see AG13), the situation is even more interesting. In this game a “capturing” move consists of traversing along an outer circuit around at least one of the eight corner loops of the board, followed by landing on an enemy piece, capturing it. Displaying a “capturing” move in a straight line from the start to the end position, as in Zillions of Games, will only confuse players—it could be confused with a “non capturing” move, although these are performed by a single step in any direction to an unoccupied point. In Dagaz, I have made animation of piece movements possible. When you make a move, whether it is straight, angled, or curved, its entire trajectory is visible, even when a piece passes over several board points in sequence. In some games, such as Surakarta, this feature is really important. In others, it is just a nice visual effect.
Lastly, when the Royal Game of Ur was first discovered, no one knew how it was played, because its rules were lost to the ages. Several historical reconstructions have been suggested, but I like these rules best, which were developed by my friend, writer and popularizer of board games, Dmitry Skiryuk. Of course, I could not pass up this game when I started Dagaz!
To sum up, I want to offer you another convenient tool for rapid implementation of board games. Dagaz continues the ideas laid down by the Zillions of Games project, but unlike Zillions Dagaz is a free product with fully open source code, available under the MIT license. My project at this time does not use a universal AI for any type of board game, but its several built-in bots can be customized for very different rules if needed. I have been working on this project for several years, so it was difficult for me to describe in this short article everything that has already been done. If you are interested in my work, please feel free to contact me. My email address is given on the Dagaz project's GitHub page.
To sum up, I want to offer you another convenient tool for rapid implementation of board games. Dagaz continues the ideas laid down by the Zillions of Games project, but unlike Zillions Dagaz is a free product with fully open source code, available under the MIT license. My project at this time does not use a universal AI for any type of board game, but its several built-in bots can be customized for very different rules if needed. I have been working on this project for several years, so it was difficult for me to describe in this short article everything that has already been done. If you are interested in my work, please feel free to contact me. My email address is given on the Dagaz project's GitHub page.