Book excerpt
Symple is a board game invented in 2010 by Christan Freeling and Benedikt Rosenau. The Dutch eminence considers it one out of six major achievements among his enormous oeuvre. When playing the game for the first time, what particularly stands out is the curious method of placing stones on the board: not one, two or any other fixed number, but a variable quantity depending on the position. This is the so-called Symple movement protocol.
What is a movement protocol?
Back in the day, this would have been a silly question. In all old games, the two players would take turns with each move being a single action for one of their own pieces.
Chess: White moves a white piece, Black moves a black piece, etc.
Go: Black places a black stone, White places a white stone, etc.
The only meaningful input is who starts, and that is just an arbitrary convention. Castling is a curious one-off double movement in Chess, not challenging the paradigm. One might think that sowing games (mancalas) deviate with their many undifferentiated seeds. But even there, a player’s action consists of emptying one pit on the player’s side.
Many interesting deviations from that traditional dogma have been invented, and some standards seem to have emerged. These are the basic types, in increasing complexity:
1. Multiple moves for single pieces.
2. Single action for many, pattern-based pieces.
3. Multiple, independent moves or placements.
Multiple moves for single pieces
Iterated jumps in the Checkers family are an early instance, and similarly with chained captures in Fanorona. Halma and Chinese Checkers take multiple jumps for movement. In the crossing game Gyges (Claude Leroy, 1985), a single piece can keep moving under certain conditions.
Single action for many, pattern-based pieces
In some games, many pieces can move at once, depending on their pattern. Examples are phalanx movement in Epaminondas (Robert Abbott, 1975), flocks in Volo (Dieter Stein, 2010) or Cannon’s cannons (David E. Whitcher, 2003). Beyond movement games, a turn in Dispatch (Chris Dissemble & João Pedro Neto, 2002) is the placement of a pentomino. All these rules provide a single, if large, action for each turn.
Many mancalas are of this type: a player chooses a pit and then proceeds to sow that pit’s seeds according to the rules. Potentially very many seeds are moved, but the player’s choice was about the pit. Some mancalas double up on this mechanic, by having the player keep sowing, always from the pit receiving previous round’s last seed. The turns take longer but I say these are still single actions because there are no further decisions involved.
Multiple, independent moves or placements
This is what I believe most people mean by "movement protocol." The reason is that such rules can, in principle, be applied to very many games—these do not depend on particular spatial or movement patterns.
A modest movement protocol beyond the old default is to allow two basic actions per turn. The alignment game Connect6 (I-Chen Wu, 2003) is a good example: players get to place two stones of their colour in each turn; except for the very first turn with only one placement. This is a smart way of fixing the second-player disadvantage in classic alignment games such as Gomoku. This movement protocol is denoted 12*, as a shorthand for 1222..., where the asterisk * indicates that the last number is repeated forever.
In fact, many games use double actions in some form, for example Slither (Corey Clark, 2010) with mandatory placement and optional movement, and Amazons (Walter Zamkauskas, 1988) with movement and shooting. Note that in these games the two basic actions are different. Another design making good use of the 12* protocol is the four-colour territorial game Blooms (Nick Bentley, 2018). The chain-scoring game Catchup (2010) by the same designer follows mostly a double-action protocol but if a player takes a lead, then the opponent is allowed three actions.
It is interesting to discuss more extravagant movement protocols for a bit. A well-known modern game is Arimaa (Omay Syed, 2002) where each turn consists of up to four actions, i.e., the 4* movement protocol. Games with turns made up of many actions work better if the single actions are simple. For example, an Arimaa action is to move one piece of the active player exactly one (orthogonal) step. Played with the 1* protocol, this would give a meaningful, if very slow, game. In the actual, 4* rules, a player can carry out up to four of these actions. In particular, the same piece can be moved several times, and it is not necessary to use up all actions. Compared to Chess with its single actions, but long-ranging pieces, the branching factor goes up tremendously. This was one design goal of Arimaa’s inventor.
Back in the day, this would have been a silly question. In all old games, the two players would take turns with each move being a single action for one of their own pieces.
Chess: White moves a white piece, Black moves a black piece, etc.
Go: Black places a black stone, White places a white stone, etc.
The only meaningful input is who starts, and that is just an arbitrary convention. Castling is a curious one-off double movement in Chess, not challenging the paradigm. One might think that sowing games (mancalas) deviate with their many undifferentiated seeds. But even there, a player’s action consists of emptying one pit on the player’s side.
Many interesting deviations from that traditional dogma have been invented, and some standards seem to have emerged. These are the basic types, in increasing complexity:
1. Multiple moves for single pieces.
2. Single action for many, pattern-based pieces.
3. Multiple, independent moves or placements.
Multiple moves for single pieces
Iterated jumps in the Checkers family are an early instance, and similarly with chained captures in Fanorona. Halma and Chinese Checkers take multiple jumps for movement. In the crossing game Gyges (Claude Leroy, 1985), a single piece can keep moving under certain conditions.
Single action for many, pattern-based pieces
In some games, many pieces can move at once, depending on their pattern. Examples are phalanx movement in Epaminondas (Robert Abbott, 1975), flocks in Volo (Dieter Stein, 2010) or Cannon’s cannons (David E. Whitcher, 2003). Beyond movement games, a turn in Dispatch (Chris Dissemble & João Pedro Neto, 2002) is the placement of a pentomino. All these rules provide a single, if large, action for each turn.
Many mancalas are of this type: a player chooses a pit and then proceeds to sow that pit’s seeds according to the rules. Potentially very many seeds are moved, but the player’s choice was about the pit. Some mancalas double up on this mechanic, by having the player keep sowing, always from the pit receiving previous round’s last seed. The turns take longer but I say these are still single actions because there are no further decisions involved.
Multiple, independent moves or placements
This is what I believe most people mean by "movement protocol." The reason is that such rules can, in principle, be applied to very many games—these do not depend on particular spatial or movement patterns.
A modest movement protocol beyond the old default is to allow two basic actions per turn. The alignment game Connect6 (I-Chen Wu, 2003) is a good example: players get to place two stones of their colour in each turn; except for the very first turn with only one placement. This is a smart way of fixing the second-player disadvantage in classic alignment games such as Gomoku. This movement protocol is denoted 12*, as a shorthand for 1222..., where the asterisk * indicates that the last number is repeated forever.
In fact, many games use double actions in some form, for example Slither (Corey Clark, 2010) with mandatory placement and optional movement, and Amazons (Walter Zamkauskas, 1988) with movement and shooting. Note that in these games the two basic actions are different. Another design making good use of the 12* protocol is the four-colour territorial game Blooms (Nick Bentley, 2018). The chain-scoring game Catchup (2010) by the same designer follows mostly a double-action protocol but if a player takes a lead, then the opponent is allowed three actions.
It is interesting to discuss more extravagant movement protocols for a bit. A well-known modern game is Arimaa (Omay Syed, 2002) where each turn consists of up to four actions, i.e., the 4* movement protocol. Games with turns made up of many actions work better if the single actions are simple. For example, an Arimaa action is to move one piece of the active player exactly one (orthogonal) step. Played with the 1* protocol, this would give a meaningful, if very slow, game. In the actual, 4* rules, a player can carry out up to four of these actions. In particular, the same piece can be moved several times, and it is not necessary to use up all actions. Compared to Chess with its single actions, but long-ranging pieces, the branching factor goes up tremendously. This was one design goal of Arimaa’s inventor.
In theory, one can apply a movement protocol such as 12* to any game. Generally, this will produce a set of rules that is worse or just does not work. For example, while 12* Chess is a cute distraction, 12* Go is a wretched monstrosity. Contrary to that, the 12* protocol is used in Connect6 to solve a problem, the disadvantage of going second in classic 1* alignment games. Note that Renju addresses this shortcoming in an entirely different way. In my opinion, the approach by Connect6 is more elegant and commendable—here the 12* protocol truly shines.
Games with long turns
Needless to say, people have pushed the envelope. An extreme case is Progressive Chess, where White starts with a single move; then Black makes two consecutive moves; White next gets three moves etc. This protocol is denoted 1234+ where the plus symbol + indicates that the sequence keeps increasing. There are special rules for check and, of course, variants. However, compared to orthodox Chess as a strategy game, this movement protocol is rather an amusing gimmick, I would say. The main website on Chess variants confirms this impression, stating that “Games are intense, and few last for more than seven successive turns.”
Out of an entirely different corner of game design, many war games (combat simulations) and computer strategy games allow the player to move many or even all units in a given turn. I believe that this tradition had repercussions on the design of abstract board games. Of course, a computer interface can make very long turns a lot more amenable. As an aside, one of the great design decisions of the early Heroes of Might & Magic computer games was to restrict movement to at most eight stacks. Not being able to micro manage every troop makes for shorter, clearer and much more meaningful turns.
Let me provide some substance for the claimed connection between multi-action war and abstract games. Of the titles mentioned below, Crosshairs has a World War I aerial fight theme, Fibonacci is science fiction war-themed, and Conquest is essentially a combinatorial war game set in the time of Rome and Carthage.
Here is a list of interesting titles having eventually three or more actions, sorted by turn length (there are very, very many double action games by now, so I skip those):
Needless to say, people have pushed the envelope. An extreme case is Progressive Chess, where White starts with a single move; then Black makes two consecutive moves; White next gets three moves etc. This protocol is denoted 1234+ where the plus symbol + indicates that the sequence keeps increasing. There are special rules for check and, of course, variants. However, compared to orthodox Chess as a strategy game, this movement protocol is rather an amusing gimmick, I would say. The main website on Chess variants confirms this impression, stating that “Games are intense, and few last for more than seven successive turns.”
Out of an entirely different corner of game design, many war games (combat simulations) and computer strategy games allow the player to move many or even all units in a given turn. I believe that this tradition had repercussions on the design of abstract board games. Of course, a computer interface can make very long turns a lot more amenable. As an aside, one of the great design decisions of the early Heroes of Might & Magic computer games was to restrict movement to at most eight stacks. Not being able to micro manage every troop makes for shorter, clearer and much more meaningful turns.
Let me provide some substance for the claimed connection between multi-action war and abstract games. Of the titles mentioned below, Crosshairs has a World War I aerial fight theme, Fibonacci is science fiction war-themed, and Conquest is essentially a combinatorial war game set in the time of Rome and Carthage.
Here is a list of interesting titles having eventually three or more actions, sorted by turn length (there are very, very many double action games by now, so I skip those):
|
2323**
3* 2424** 4* 1122334455* 123456* 112233++ |
Chain Lightning
Push Fight Unfair Arimaa Crosshairs Fibonacci Mu Velox |
(Andrew Juell, 2010)
(Brett Picotte, 2008) (Stephen Tavener, 2015) (Omar Syed, 2002) (Stephen Tavener, 2010) (Thomas Naylor, 1990) (Christian Freeling, 1986) |
The rules may assign different numbers of actions to each side. Of the games in the table, Chain Lightning is an asymmetric connection game and Unfair is an asymmetric alignment game. For all games listed, there is rule-given upper limit on the number of actions. For Mu Velox, the precursor to Storisende, this is not obvious but a player gets to move one piece from each segment controlled by the player at the start of a turn.
The branching explosion
While any conflated-moves protocol can be applied to an existing game, results will be mixed. Beyond 12* Go, someone might come up with Progressive Go, i.e., Go with the 1234+ protocol; obviously, this is a bizarre failure of a game.
The branching explosion
While any conflated-moves protocol can be applied to an existing game, results will be mixed. Beyond 12* Go, someone might come up with Progressive Go, i.e., Go with the 1234+ protocol; obviously, this is a bizarre failure of a game.
So it is not easy to make a good multi-action abstract board game, for two reasons: First, the rules should work seamlessly without computer aid. With long turns, this can become problematic. Second, multi-action turns increase the branching rate drastically—far more so than increasing the board size! For example, consider a pure placement game such as Gomoku or Hex on an N×N board. With the standard 1* protocol, the branching rate is N2. Doubling the length of the board increases the branching rate to (2N)2, yielding an increase by factor 4. But keeping the N × N board and using the 2* protocol leads to a branching rate of N4. While this is often the desired design goal, it hampers clarity if done carelessly: players simply cannot plan ahead meaningfully.
Through this branching explosion, I believe that speeding up a game, for instance by going from 1* to 12*, often ramps up tactical depth. However, I am skeptical about strategic heuristics, and worry that a game not designed for a particular protocol will suffer and have its strategic concepts undermined. One way to deal with this is by accompanying a faster movement protocol with restrictions. This train of thought is explored in the article "Mutators for Restrictive Game Play" by João Pedro Neto and Bill Taylor (Game & Puzzle Design, Vol. 1, No. 1 (2015), pp. 1–3).
Non-partisan movement and placement
There is a different way in which the traditional movement protocol can be opened up: instead of having a player only move or place pieces of that player’s colour, it could allow the other colour or, for multi-action protocols, both. For example, in Xodd (Luis Bolaños Mures, 2011), a player’s turn consists of placing two stones of either colour on empty points (except for the very first turn which is only a single placement).
Going beyond that, some games have stones or pieces belonging to neither player. There are some interesting designs of that kind but I adhere to the old-fashioned Manichaean school where pieces are either black or white, and so I will not dwell on such games. Interesting and fun games of that kind are Nex (João Pedro Neto, 2004), Santorini (Gordon Hamilton, 2004), and Iquishiqui (João Pedro Neto & Bill Taylor, 2003).
Action points
Yet another approach to generalized movement is an action-point system. This means that for each turn, a player has a contingent of points to spend on various actions which can have different costs. This device is often used in proprietary, themed strategy board games. But some of them behave, when restricted to two players, just like abstract games with perfect information and no chance elements.
I mention four examples: Hare & Tortoise (David Parlett, 1973) is a racing game with an action-point engine. Conquest (Donald Benge, 1974) has 20 action points to use on its chariots, elephants, and other units. Quite famous is Torres (Michael Kiesling & Wolfgang Kramer, 1999) which, as a two-player game with the master rules, is a luckless tower-scoring game with five action points per turn. And Terra Nova (Gaetano Evola & Rosanna Leocata, 2006) is a themed area majority game with three action points per turn.
To me, elaborate systems with many action types are less elegant than sequences of one or two basic actions; similarly, I prefer visual scoring of areas or captives over intricate victory point systems. Irrespective of my opinion, some inventors came up with movement protocols that allow very long sequences of simple basic actions. Of course, there will almost always be an upper bound to turn length, dictated by the dimensions of the board: here I am looking for games where the number of actions (a) can become large, and (b) is not a priori capped by the rules. I will move towards Symple by focusing on games with massive turns
Non-partisan movement and placement
There is a different way in which the traditional movement protocol can be opened up: instead of having a player only move or place pieces of that player’s colour, it could allow the other colour or, for multi-action protocols, both. For example, in Xodd (Luis Bolaños Mures, 2011), a player’s turn consists of placing two stones of either colour on empty points (except for the very first turn which is only a single placement).
Going beyond that, some games have stones or pieces belonging to neither player. There are some interesting designs of that kind but I adhere to the old-fashioned Manichaean school where pieces are either black or white, and so I will not dwell on such games. Interesting and fun games of that kind are Nex (João Pedro Neto, 2004), Santorini (Gordon Hamilton, 2004), and Iquishiqui (João Pedro Neto & Bill Taylor, 2003).
Action points
Yet another approach to generalized movement is an action-point system. This means that for each turn, a player has a contingent of points to spend on various actions which can have different costs. This device is often used in proprietary, themed strategy board games. But some of them behave, when restricted to two players, just like abstract games with perfect information and no chance elements.
I mention four examples: Hare & Tortoise (David Parlett, 1973) is a racing game with an action-point engine. Conquest (Donald Benge, 1974) has 20 action points to use on its chariots, elephants, and other units. Quite famous is Torres (Michael Kiesling & Wolfgang Kramer, 1999) which, as a two-player game with the master rules, is a luckless tower-scoring game with five action points per turn. And Terra Nova (Gaetano Evola & Rosanna Leocata, 2006) is a themed area majority game with three action points per turn.
To me, elaborate systems with many action types are less elegant than sequences of one or two basic actions; similarly, I prefer visual scoring of areas or captives over intricate victory point systems. Irrespective of my opinion, some inventors came up with movement protocols that allow very long sequences of simple basic actions. Of course, there will almost always be an upper bound to turn length, dictated by the dimensions of the board: here I am looking for games where the number of actions (a) can become large, and (b) is not a priori capped by the rules. I will move towards Symple by focusing on games with massive turns
Protocols allowing very long turns
Could Progressive Chess or, more generally, the 1234+ protocol applied to any game, be an example? No: Chess was designed for the traditional 1* and, as the above quote about Progressive Chess shows, turns do not become very long in that variant. I am not aware of any game that works well with this protocol. There are two deeper reasons why 1234+ is flawed in itself, independently of Chess: First, in a game using this protocol and having long matches, players are forced to count (or otherwise keep track of) the allowed number of actions; this is tedious. But second, this means that the action contingent is not intrinsic: an observer arriving at the game could not infer from the board position how many actions a player has.
So here I want to focus on games that have been specifically designed with very long turns in mind. The following three movement protocols have this property, and they allow for long turns in intrinsic and natural ways. Also, they are protocols in the sense that they, in principle, apply to many games.
I am using the word chain to mean a maximal set of one-coloured pieces which are connected to each other. This is called "clump" in Lines of Action, "chunk" in Wunchunk below, and "group" in many games. (But not in Go, where "group" is a looser concept, a set of stones considered as a unit.) This concept is crucial for connection games such as Hex where players win by building a chain linking certain edges. There are also many point scoring games which assign score values depending in some way on the distribution of chain sizes after game end.
Could Progressive Chess or, more generally, the 1234+ protocol applied to any game, be an example? No: Chess was designed for the traditional 1* and, as the above quote about Progressive Chess shows, turns do not become very long in that variant. I am not aware of any game that works well with this protocol. There are two deeper reasons why 1234+ is flawed in itself, independently of Chess: First, in a game using this protocol and having long matches, players are forced to count (or otherwise keep track of) the allowed number of actions; this is tedious. But second, this means that the action contingent is not intrinsic: an observer arriving at the game could not infer from the board position how many actions a player has.
So here I want to focus on games that have been specifically designed with very long turns in mind. The following three movement protocols have this property, and they allow for long turns in intrinsic and natural ways. Also, they are protocols in the sense that they, in principle, apply to many games.
I am using the word chain to mean a maximal set of one-coloured pieces which are connected to each other. This is called "clump" in Lines of Action, "chunk" in Wunchunk below, and "group" in many games. (But not in Go, where "group" is a looser concept, a set of stones considered as a unit.) This concept is crucial for connection games such as Hex where players win by building a chain linking certain edges. There are also many point scoring games which assign score values depending in some way on the distribution of chain sizes after game end.
|
The Wunchunk protocol
The player may place one stone for each chain of that player’s colour of size two or more. |
The Oust protocol
The player carries out any number (including zero) of capturing moves, followed by a single non-capturing move. |
The Symple protocol
The player either places a stone as a size one chain ("plant") or extends each existing chain of the player’s colour by one stone ("grow"). |
In actual play
An obvious question is how to carry out these turns in analogue games, i.e. without computer aid. This is not a problem at all for the Oust protocol, and easy for Symple: for growth turns, simply place auxiliary markers such as coins and replace them with actual pieces at the end. This allows for a convenient check that the proposed move is correct and desirable. This also works for the Wunchunk protocol: place auxiliary markers and before replacing them with actual stones, quickly check that their number corresponds to chunks.
Immediate comments
The Oust protocol is certainly inspired by Dots & Boxes, a perennial application of squared paper in classrooms. In the latter game, closing ("capturing") one square allows (and forces) another move. For example, Mark Steere’s Flume (2010) is another board game strongly related to Dots & Boxes. I have chosen Oust because it is a placement game with capture (making the protocol more universal) and it is an elimination game starting on an empty board, which is quite unusual.
The Wunchunk and Symple protocols generate actions depending on the number of chains of the active player. The differences are: (a) placement is free in Wunchunk and restricted to growing chains in Symple (the latter is a very natural restriction) and (b) when counting actions, Wunchunk disregards single-stone chains. There are a lot of possible variations but I believe these two protocols give a good impression of what I mean by "long turns," "‘intrinsic," and"natural."
An obvious question is how to carry out these turns in analogue games, i.e. without computer aid. This is not a problem at all for the Oust protocol, and easy for Symple: for growth turns, simply place auxiliary markers such as coins and replace them with actual pieces at the end. This allows for a convenient check that the proposed move is correct and desirable. This also works for the Wunchunk protocol: place auxiliary markers and before replacing them with actual stones, quickly check that their number corresponds to chunks.
Immediate comments
The Oust protocol is certainly inspired by Dots & Boxes, a perennial application of squared paper in classrooms. In the latter game, closing ("capturing") one square allows (and forces) another move. For example, Mark Steere’s Flume (2010) is another board game strongly related to Dots & Boxes. I have chosen Oust because it is a placement game with capture (making the protocol more universal) and it is an elimination game starting on an empty board, which is quite unusual.
The Wunchunk and Symple protocols generate actions depending on the number of chains of the active player. The differences are: (a) placement is free in Wunchunk and restricted to growing chains in Symple (the latter is a very natural restriction) and (b) when counting actions, Wunchunk disregards single-stone chains. There are a lot of possible variations but I believe these two protocols give a good impression of what I mean by "long turns," "‘intrinsic," and"natural."
|
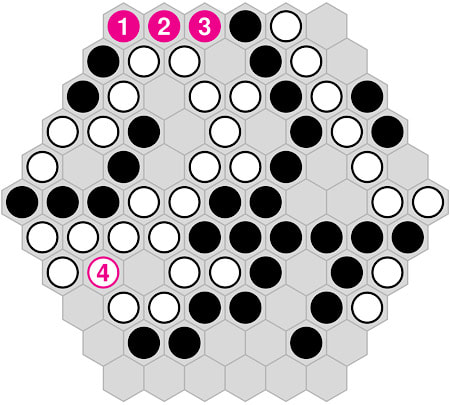
Wunchunk (Craig Duncan, 2019)
The game is played on a six-sided hex board of size 6 or more with the shown initial position. Chains of two or more same-coloured stones are called chunks; each player has a chunk count at any time. On a turn, a player places at most chunk-count many stones on empty hexes; placing no stones is allowed and a pass. Each stone placed can be of either colour. The game ends when both players pass in succession or when the board is full. The winner is the player with the smaller chunk count. If these are equal, then the fewer number of smallest chains win. This is checked recursively: first the number of singletons is compared; if equal, the number of size two chains are compared, etc. Black goes first and the pie rule is used. |
Clearly, this game is driven by the tension between building many chunks, which allows for strong turns, yet the win going to the smaller number of chunks. The rules of Wunchunk allow the placement of stones of either colour; this is a design decision independent of the movement protocol. By the way, the game is designed for up to four players.
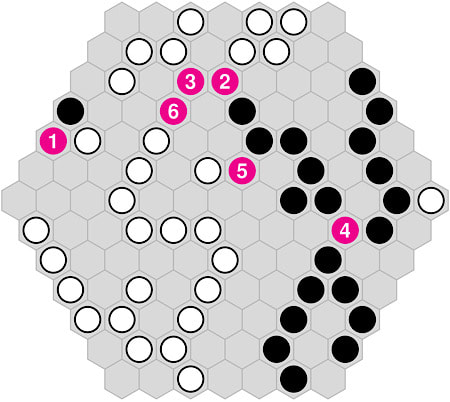
Oust (Previously called Hex Oust, this is the designer’s official version.) (Mark Steere, 2007)
The game is played on a six-sided hexagonal board, initially empty. Players take turns placing at least one stone of their colour on an empty hexagon. There are two types of placement:
1. Silent: the new stone is not adjacent to any like-coloured stone.
2. Capture: the new stone is adjacent to like-coloured stones. This is only allowed if (a) the resulting chain is adjacent to at least one opposing chain and (b) is larger than all adjacent opposing chains. In this case, all adjacent opposing chains are removed.
Each capture placement has to be followed by a further placement until the player finally makes a silent placement. A player unable to place a stone has to pass (and in this situation the opponent will be able to make a move). A player wins by removing all opposing stones from the board.
The game is played on a six-sided hexagonal board, initially empty. Players take turns placing at least one stone of their colour on an empty hexagon. There are two types of placement:
1. Silent: the new stone is not adjacent to any like-coloured stone.
2. Capture: the new stone is adjacent to like-coloured stones. This is only allowed if (a) the resulting chain is adjacent to at least one opposing chain and (b) is larger than all adjacent opposing chains. In this case, all adjacent opposing chains are removed.
Each capture placement has to be followed by a further placement until the player finally makes a silent placement. A player unable to place a stone has to pass (and in this situation the opponent will be able to make a move). A player wins by removing all opposing stones from the board.
The rules of Symple are given in the next section. For both Wunchunk and Symple, the movement protocol is largely independent of the chain-scoring win condition. And indeed, Christian Freeling later designed the connection game Scware and the territory-scoring game Sygo on the Symple protocol. Actually, Phalanx is another territorial game by the same author combining a grow-or-move extension of the Symple protocol with Epaminondas-style captures. Benedikt Rosenau applied the Symple protocol to Hex with no other changes except also replacing the swap rule by Symple’s balancing mechanic, giving rise to Symple Hex. With Itsy, Stephen Tavener twisted the Symple protocol to make a first-capture variant of Go. And while less universal than the other two protocols, the Oust core concept can certainly be used in other games. Here are three examples for turns in these games:
It is worthwhile to point out at that Symple and Oust are very cold games. This means that zugzwang, i.e., the compulsion to make a legal move, comes up in almost every match, and has to be part of a player’s reasoning from early on. However, while zugzwang is indispensable to Oust, allowing to pass in Symple would give still a reasonable game, in my opinion. In fact, the two designers of Symple disagreed on that point, as well.
Symple, the game
Christian Freeling regards Symple as one of his major achievements, along with Grand Chess, Dameo, Emergo, Sygo, and Storisende. Symple can be played online at mindsports.nl and against Stephen Tavener’s AiAi program; doing either also conveniently keeps track of scores.
Christian Freeling regards Symple as one of his major achievements, along with Grand Chess, Dameo, Emergo, Sygo, and Storisende. Symple can be played online at mindsports.nl and against Stephen Tavener’s AiAi program; doing either also conveniently keeps track of scores.
Symple (Christian Freeling & Benedikt Rosenau, 2010)
The game is played on a square board, initially empty. Before game start, players agree on an integer value P. White goes first. On a turn, a player must either
plant: place a stone on a vacant point having no adjacent stones of the same colour, or
grow: extend each chain of the player’s colour by exactly one stone, if possible.
As long as no player has grown yet, Black may first grow and then plant in a single turn.
The game ends if the board is full. At that point, the score of each player is the number of stones placed minus P points for each chain of that player’s colour. The winner is the player with the higher score.
The game is played on a square board, initially empty. Before game start, players agree on an integer value P. White goes first. On a turn, a player must either
plant: place a stone on a vacant point having no adjacent stones of the same colour, or
grow: extend each chain of the player’s colour by exactly one stone, if possible.
As long as no player has grown yet, Black may first grow and then plant in a single turn.
The game ends if the board is full. At that point, the score of each player is the number of stones placed minus P points for each chain of that player’s colour. The winner is the player with the higher score.
Diagrams explaining the rules
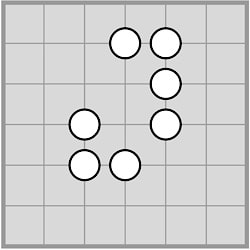
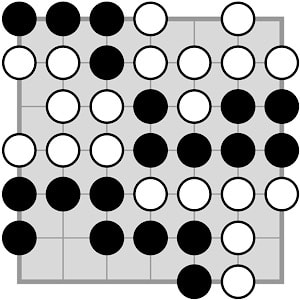
Symple is eminently scalable, and diagrams will use 7 × 7 boards.
Symple is eminently scalable, and diagrams will use 7 × 7 boards.
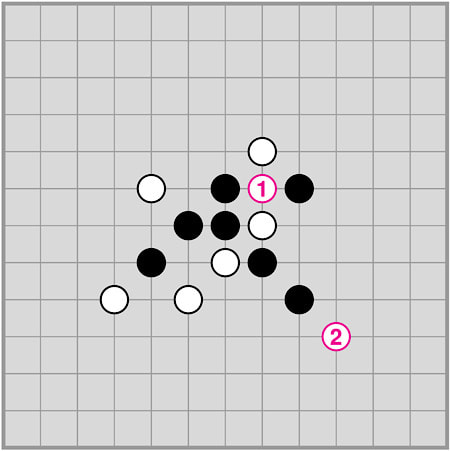
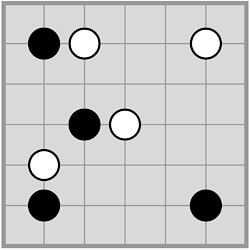
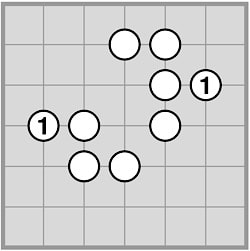
The next set of diagrams show valid growth moves for the two white chains shown. Note that in the right-hand diagram, each of the new stones extends just one chain of the starting diagram.
The meaning of the penalty P
The rules don’t specify the chain penalty for scoring. I do not like keeping players in the dark about such options when they want to try out a game, so here are defaults which work well:
The rules don’t specify the chain penalty for scoring. I do not like keeping players in the dark about such options when they want to try out a game, so here are defaults which work well:
9 × 9 board: P = 4, 13 × 13 board: P = 6, 19 × 19 board: P = 10
The designers consider the choice of P as part of the game. On odd-sized boards, even numbered P prevents draws. As so often, it is interesting to ponder extreme cases on an N × N board:
P = 0 — In this case, the goal is to maximize stone count at the end of the game.
P = N2 — Win by smaller number of chains; equality is broken by number of stones.
P = -N2 — Win by larger number of chains; equality is broken by number of stones.
Curiously, none of these extreme variants leads to degenerate, entirely trivial games. Without going into details, this follows from the plant/grow protocol, cutting, and connections, and the resulting cold phase (if P ≠ 0). That forebodes well for the real game with modest penalties!
It is even more curious to compare Symple with Weiqi (Go) scoring in ancient China: they used to add up surrounded points and count prisoners—as in modern Japanese scoring. However, a player would hand two prisoners to the opponent for each group. This is very similar to Symple scoring with a penalty P = 2! (There is a minor distinction in that Go groups are not the same thing as chains.) Clearly, these two stones represent the two eyes a group needs to live.
Plant vs. grow
In Symple, the goal is to get as many stones on the board as possible in as few chains as possible. This dilemma carries the game to a large extent: having more chains is good for further growth, hence points, but it becomes a liability due to the score penalty for each chain. Because players have to move, running out of growth options means that a player is forced to plant inside an opposing territory. The new stone may not out-grow the chain penalty, and thus incur a loss. Therefore, most matches have a cold phase, where players try to delay or avoid negative moves. This leads to a nuanced middle game. Roughly speaking, Symple games proceed like this:
1. Opening: planting moves exclusively.
2. Midgame: from first growth until territories are traced out. Border battles and invasions.
3. Endgame: territory filling and connections. Cold phase.
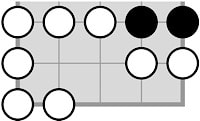
Growth order matters
It can happen that a particular choice of growth prevents another chain from growing. For example, White can fill the corner area in three, four or five turns. Filling a region as slowly as possible can be important, especially in a localized shape such as this: during a cold phase both players strive to avoid having to plant a new stone in an opposite territory.
It is even more curious to compare Symple with Weiqi (Go) scoring in ancient China: they used to add up surrounded points and count prisoners—as in modern Japanese scoring. However, a player would hand two prisoners to the opponent for each group. This is very similar to Symple scoring with a penalty P = 2! (There is a minor distinction in that Go groups are not the same thing as chains.) Clearly, these two stones represent the two eyes a group needs to live.
Plant vs. grow
In Symple, the goal is to get as many stones on the board as possible in as few chains as possible. This dilemma carries the game to a large extent: having more chains is good for further growth, hence points, but it becomes a liability due to the score penalty for each chain. Because players have to move, running out of growth options means that a player is forced to plant inside an opposing territory. The new stone may not out-grow the chain penalty, and thus incur a loss. Therefore, most matches have a cold phase, where players try to delay or avoid negative moves. This leads to a nuanced middle game. Roughly speaking, Symple games proceed like this:
1. Opening: planting moves exclusively.
2. Midgame: from first growth until territories are traced out. Border battles and invasions.
3. Endgame: territory filling and connections. Cold phase.
Growth order matters
It can happen that a particular choice of growth prevents another chain from growing. For example, White can fill the corner area in three, four or five turns. Filling a region as slowly as possible can be important, especially in a localized shape such as this: during a cold phase both players strive to avoid having to plant a new stone in an opposite territory.
The slowest approach is to connect as early as possible. In a bigger position, matters are more subtle: regarding points on the whole board, delayed connections are preferable.
Second mover compensation
Black has the privilege of growing and planting, but only if neither player has grown before. This is a compensation for going second, and creates some tension in its own right: in principle, both sides want to delay growth and start planting. But if White does that for too long, then Black will carry out the double action. This provides incentive for White to grow sooner than otherwise intended, which in turn does the same for Black!
As an example, it is not a good idea for Black to use the double action privilege on turn 2. By doing so, Black has placed one more stone but now White can plant without having to worry about a later grow and plant by Black.
Optimizing agriculture
Now focus on the stone-maximizing part. Obviously, any optimal procedure would start with planting a number of stones, and then keep on growing.
So assume starting with n turns planting stones, followed by m turns of growing. This leads to n(m + 1) stones after n + m turns. Also assume that play takes place on a 13 × 13 board and the goal is to reach at least 80 stones, which is roughly half of it. Here are some possibilities:
Second mover compensation
Black has the privilege of growing and planting, but only if neither player has grown before. This is a compensation for going second, and creates some tension in its own right: in principle, both sides want to delay growth and start planting. But if White does that for too long, then Black will carry out the double action. This provides incentive for White to grow sooner than otherwise intended, which in turn does the same for Black!
As an example, it is not a good idea for Black to use the double action privilege on turn 2. By doing so, Black has placed one more stone but now White can plant without having to worry about a later grow and plant by Black.
Optimizing agriculture
Now focus on the stone-maximizing part. Obviously, any optimal procedure would start with planting a number of stones, and then keep on growing.
So assume starting with n turns planting stones, followed by m turns of growing. This leads to n(m + 1) stones after n + m turns. Also assume that play takes place on a 13 × 13 board and the goal is to reach at least 80 stones, which is roughly half of it. Here are some possibilities:
So at least 17 turns are necessary to stake out 80 points, and there are three possibilities for this planting 8, 9 or 10 turns before switching to growth. It seems reasonable that nearby values, such as planting for 7, 11 or 12 turns should also be relevant for good play. All of this supposes that the chains can grow enough—early on, this should be a valid assumption although it is possible to play a close-contact game right away, forcing earlier growth moves than in spaced-out, large-scale openings.
Analysis of an endgame position
Let us look closely at a Symple endgame position. This will exhibit the following concepts, although on a tiny scale: cold phase, invasions, defensive planting. The combinatorial complexity becomes enormous for more open positions, and one has to rely on heuristics.
In analysing this position, start with the most naïve approach: both sides just keep growing. In the next step, one has to consider invasions (offensive plantings), counter-invasions, and defensive moves (both growth and planting). This holds for endgame positions. As usual for board games, the opening and middle game are less scripted.
Analysis of an endgame position
Let us look closely at a Symple endgame position. This will exhibit the following concepts, although on a tiny scale: cold phase, invasions, defensive planting. The combinatorial complexity becomes enormous for more open positions, and one has to rely on heuristics.
In analysing this position, start with the most naïve approach: both sides just keep growing. In the next step, one has to consider invasions (offensive plantings), counter-invasions, and defensive moves (both growth and planting). This holds for endgame positions. As usual for board games, the opening and middle game are less scripted.
|
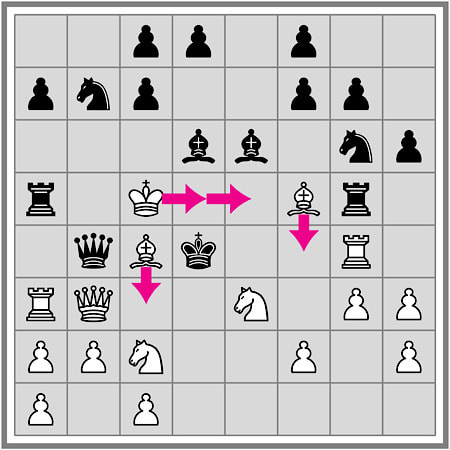
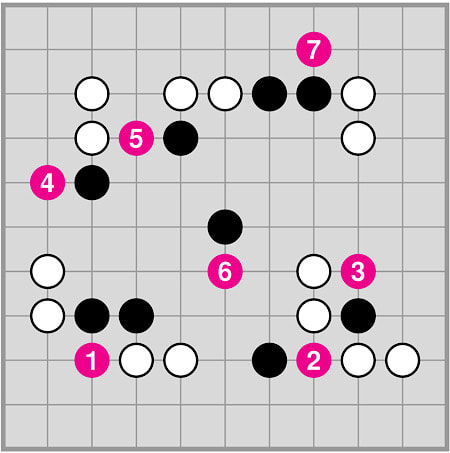
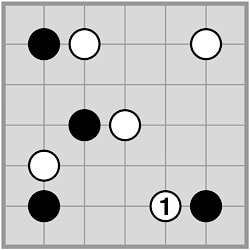
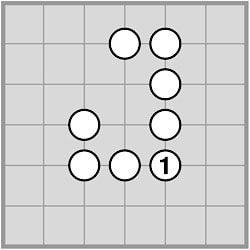
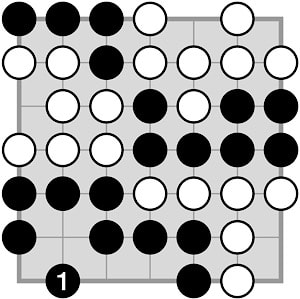
Consider the position on the right: Black to play, P = 4.
Chain sizes: 7 + 7 + 6 = 20 for White and 4 + 7 + 8 = 19 for Black. There are precisely three chains of each colour which cannot con- nect anywhere. Moreover, both sides enclose 5 points in their areas, but—and this is an important difference—these make up a single black territory while they are distributed over three white areas. |
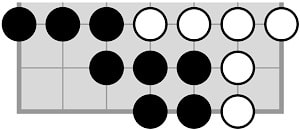
|
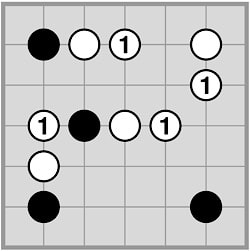
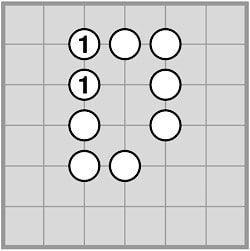
Black grows and White invades immediately: So White must do better: being forced to plant inside Black’s territory anyway, it is best to do it immediately and make the invading chain as large as possible. This secures a one point win for White: Black: 22 − 3 · 4 = 10 points, White: 27 − 4 · 4 = 11 points. Instead of 2, White can also invade on the point to its right. |
|
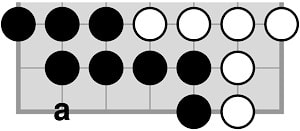
Black’s correct move is defensive planting: Therefore, in the original position 1 should be planted inside the Black territory. Now White will not be able to grow the invading stone, and hence lose. It is left to the reader to check what happens if White keeps on planting inside Black’s corner. In an actual game, on a bigger board, it depends on overall circumstances when a defensive planting move like 1 is appropriate. |
|
This solution hinges on the shape of Black’s lower left corner. With the 5 point area shown here, no black placement can prevent White’s invasion and subsequent growth. In this position, Black will lose, assuming that White plays optimally. And if the lower left region had a more favourable shape, then a growth move at a would have sufficed. This indicates that early defensive growths can prove very beneficial in the long run: aim for flat, linear regions rather than compact, square-shaped ones. |
Conclusion
Hopefully I could convince you that discussing movement protocols in general, and Symple in particular, is worth your time. Needless to say, this article only scratches the surface. Much more could and should be said, and also about so many other games. Perhaps you may want to scrutinize a game of your liking!
Hopefully I could convince you that discussing movement protocols in general, and Symple in particular, is worth your time. Needless to say, this article only scratches the surface. Much more could and should be said, and also about so many other games. Perhaps you may want to scrutinize a game of your liking!