Connection games
Qua is an ingenious three-dimensional (3D) connection game for three players. The Qua game board is a 3D grid of cells called a Qua Cube. The game uses three different identifying marks, called qua, one for each player. The Qua Cube does not start out empty. Some of its cells are permanently filled in with one of these three qua. A qua has colour and shape and is also used to identify a player’s ownership of opposite faces on the Qua Cube game board and their game-play pieces. One set of choices for qua are yellow circles, blue squares, and white triangles modified slightly to form the letters Q, U, and A, as shown in the title, above.
Qua Game Board Layout
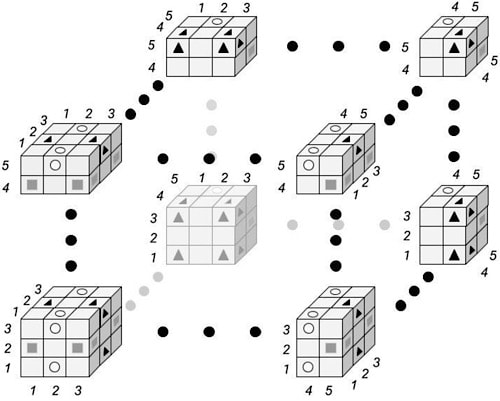
An alternative choice for qua are white circles, gray squares and black triangles, as shown in Diagram 1. The starting position for a 3x3x3 game of Qua is shown in the lower left. The starting position for a 5x5x5 game is constructed by repeating the permanent qua pattern of filled in cells in all three orthogonal directions.
Qua Game Board Layout
An alternative choice for qua are white circles, gray squares and black triangles, as shown in Diagram 1. The starting position for a 3x3x3 game of Qua is shown in the lower left. The starting position for a 5x5x5 game is constructed by repeating the permanent qua pattern of filled in cells in all three orthogonal directions.
A Qua Cube game board can be of arbitrary size and has an NxNxN cube structure composed of N3 cells. Each of these cells are 1x1x1 cubes. A cell is adjacent to a neighbouring cell if it shares a cell face with it. N2 cells in the shape of a square are adjacent to each of the six Qua Cube faces. N cells in a straight line form a Qua Cube edge, where each of the 12 edges are adjacent to two Qua Cube faces. One cell in each of the eight Qua Cube corners are adjacent to three different Qua Cube faces.
For the 5x5x5 Qua Cube game board, 54 cells are initially filled-in with qua and 71 cells are empty.
The assignment of cube faces to players is not shown in Diagram 1. Left and right cube faces belong to the White Circle player. Front and back cube faces belong to the Black Triangle player. Top and bottom cube faces belong to the Gray Square player.
Rules
At the start of a game, players choose their qua and decide who will go first, second and third. Players take turns placing qua in an empty cell, which must be adjacent to two cells already containing their qua or one such cell and one of their cube faces. This forms or adds to a chain of qua in either a straight line or right angle turn, depending on which cells are adjacent to the cell being occupied by a player that turn.
The first player to complete a chain of qua that connects their two cube faces wins.
Notes
The assignment of cube faces to players is not shown in Diagram 1. Left and right cube faces belong to the White Circle player. Front and back cube faces belong to the Black Triangle player. Top and bottom cube faces belong to the Gray Square player.
Rules
At the start of a game, players choose their qua and decide who will go first, second and third. Players take turns placing qua in an empty cell, which must be adjacent to two cells already containing their qua or one such cell and one of their cube faces. This forms or adds to a chain of qua in either a straight line or right angle turn, depending on which cells are adjacent to the cell being occupied by a player that turn.
The first player to complete a chain of qua that connects their two cube faces wins.
Notes
The initial arrangement of qua in the 5x5x5 Qua Cube game board shown in Diagram 1 guarantees there will always be a winner. This is true for all Qua Cube game boards using the same arrangement pattern for odd values of N. For an NxNxN Qua Cube, 3 x (N-1)/2 x ((N+1)/2)2 cells are initially filled-in using the rotationally symmetric pattern shown in Diagram 1. Hidden from view are cells on the left, back and bottom of the eight parts. The qua for these hidden cells are identical to corresponding cells on the right, front, and top.
Strategy and Tactics
Because this is a three-player game, the second player does not need to block single threats by the first player, the third player does not need to block single threats by the second player and the first player does not need to block single threats by the third player. However, if the player before you makes a double threat, block the one the next player cannot block, if there is one.
In a 3x3x3 Qua game, the first player has a significant advantage. The second and third players need to cooperate to avoid a quick win by the first player. For the 3x3x3 Qua game, if the first player’s first move is to occupy a cube corner cell, the second player’s first move should be to occupy the 3D orthogonally opposite cube corner cell.
If the player before you makes a threat, it is important to notice and block it if it cannot be blocked by the next player. Avoid making threats when the next player can make a double threat of their own. When in doubt, take away the next player’s best move.
History
Martha Pidcock came up with the game idea in 2016 as a 3D extension of the Game of Gale (Gardner, 1987, p.84), marketed as Bridg-It (Browne, 2005, p.15-17). The novel idea involved combining the identifiers for bridges and posts into a single identifying mark, and replacing the interspersed grids of pegs with a single 3D matrix of cells. Also, instead of having end posts along the sides of the board, these were replaced by assigning the identifying marks to cube faces. For a more detailed description on how this was done, see the Appendix.
In 2019, Sherwood Pidcock prototyped the 3D game on a 3D printer and named it Qua® (Pidcock, 2019). A prototype of the Qua Game is shown in the picture below. The Yellow Circles (Q) player wins by completing a chain from left to right; the Blue Squares (U) player wins by completing a chain from top to bottom; the White Triangles (A) player wins by completing a chain from front to back.
Because this is a three-player game, the second player does not need to block single threats by the first player, the third player does not need to block single threats by the second player and the first player does not need to block single threats by the third player. However, if the player before you makes a double threat, block the one the next player cannot block, if there is one.
In a 3x3x3 Qua game, the first player has a significant advantage. The second and third players need to cooperate to avoid a quick win by the first player. For the 3x3x3 Qua game, if the first player’s first move is to occupy a cube corner cell, the second player’s first move should be to occupy the 3D orthogonally opposite cube corner cell.
If the player before you makes a threat, it is important to notice and block it if it cannot be blocked by the next player. Avoid making threats when the next player can make a double threat of their own. When in doubt, take away the next player’s best move.
History
Martha Pidcock came up with the game idea in 2016 as a 3D extension of the Game of Gale (Gardner, 1987, p.84), marketed as Bridg-It (Browne, 2005, p.15-17). The novel idea involved combining the identifiers for bridges and posts into a single identifying mark, and replacing the interspersed grids of pegs with a single 3D matrix of cells. Also, instead of having end posts along the sides of the board, these were replaced by assigning the identifying marks to cube faces. For a more detailed description on how this was done, see the Appendix.
In 2019, Sherwood Pidcock prototyped the 3D game on a 3D printer and named it Qua® (Pidcock, 2019). A prototype of the Qua Game is shown in the picture below. The Yellow Circles (Q) player wins by completing a chain from left to right; the Blue Squares (U) player wins by completing a chain from top to bottom; the White Triangles (A) player wins by completing a chain from front to back.
Dice Qua
Players roll a die to decide which qua they will play each turn. A player may win on an opposing player’s turn!
Dice Qua is also a way to play the game with two players. Players choose their qua at the start of the game and then roll a die each turn to determine which qua game play piece to play. A player wins when a complete chain of their qua connects their two cube faces. This may happen on the opponent’s turn. If the unselected third player’s qua completes a chain between its two cube faces, play continues. The game is a draw if neither of the game’s players has a complete chain between their two cube faces before all the empty cells on the game board are filled (unlikely).
References
Browne, C. B. (2005). Connection games: Variations on a theme. Wellesley, MA: A K Peters.
Gardner, M. (1987). The 2nd SCIENTIFIC AMERICAN book of mathematical puzzles & diversions. Chicago, IL: The University of Chicago Press.
Pidcock, S. C. (2019). Qua, Retrieved February 11, 2020.
Appendix: Extending Bridg-It into 3D to create the Game of Qua
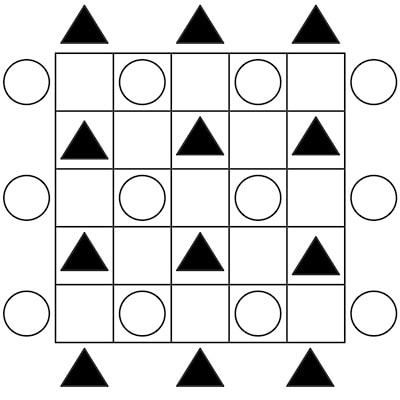
Diagram 2 shows a 3x3 Bridg-It game board with interspersed grids of black and white pegs. In Bridg-It, players take turns placing a bridge that connects two pegs of their colour and goes between two pegs of the opposing player’s colour, blocking them from becoming connected (Browne, 2005, p. 15).
Players roll a die to decide which qua they will play each turn. A player may win on an opposing player’s turn!
Dice Qua is also a way to play the game with two players. Players choose their qua at the start of the game and then roll a die each turn to determine which qua game play piece to play. A player wins when a complete chain of their qua connects their two cube faces. This may happen on the opponent’s turn. If the unselected third player’s qua completes a chain between its two cube faces, play continues. The game is a draw if neither of the game’s players has a complete chain between their two cube faces before all the empty cells on the game board are filled (unlikely).
References
Browne, C. B. (2005). Connection games: Variations on a theme. Wellesley, MA: A K Peters.
Gardner, M. (1987). The 2nd SCIENTIFIC AMERICAN book of mathematical puzzles & diversions. Chicago, IL: The University of Chicago Press.
Pidcock, S. C. (2019). Qua, Retrieved February 11, 2020.
Appendix: Extending Bridg-It into 3D to create the Game of Qua
Diagram 2 shows a 3x3 Bridg-It game board with interspersed grids of black and white pegs. In Bridg-It, players take turns placing a bridge that connects two pegs of their colour and goes between two pegs of the opposing player’s colour, blocking them from becoming connected (Browne, 2005, p. 15).
White’s sides are left and right; Black’s sides are front and back. The Bridg-It game in Diagram 2 has 9 + 4 = 13 possible bridge placement locations, where either the White player or the Black player can place a bridge to connect their pegs while blocking the other player from doing the same. Placement of a bridge at nine of these locations goes perpendicular to the player’s two sides, and placement of a bridge at the other four locations goes parallel to the player’s two sides. To extend this into 3D, imagine gray pegs above and below the nine locations where bridge placement will be perpendicular to a player’s sides. A third Gray player placing a vertical bridge at any of these 9 locations would block both the White player and Black player from placing a bridge at that location. Note that a bridge placement at these locations by this Gray player would be perpendicular to the bottom and top faces of an imagined cube, which would belong to the Gray player.
A bridge placed by the White or Black player at the other four bridge placement locations in Diagram 2 are parallel to these players’ two sides. Since the Gray player cannot place a bridge to connect two gray pegs at these locations parallel to the gray player’s two cube faces, only the White player or Black player can place a bridge at these locations.
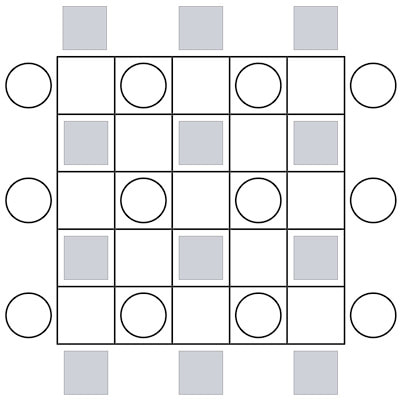
The Bridg-It game board shown in Diagram 2 is redrawn in Diagram 3 using circles and triangles instead of pegs, and the pegs along the sides are placed outside of a 5 x 5 square matrix.
A bridge placed by the White or Black player at the other four bridge placement locations in Diagram 2 are parallel to these players’ two sides. Since the Gray player cannot place a bridge to connect two gray pegs at these locations parallel to the gray player’s two cube faces, only the White player or Black player can place a bridge at these locations.
The Bridg-It game board shown in Diagram 2 is redrawn in Diagram 3 using circles and triangles instead of pegs, and the pegs along the sides are placed outside of a 5 x 5 square matrix.
This representation facilitates extending Bridg-It into 3D by replacing the white and black overlapping rectangular grids with a 5x5 square composed of empty cells and cells filled-in with white circles and black triangles. The 13 bridge placement locations from Diagram 2 become the 13 empty cells inside the 5x5 square game board shown in Diagram 3. The white circles and black triangles outside this game board, which identify the sides of the game board belonging to the White Circle and Black Triangle players, will be removed.
Using the terminology Layers, Ranks and Files will help describe 3D orientations when forming the Qua Cube game board extension to the Bridg-It Square game board.
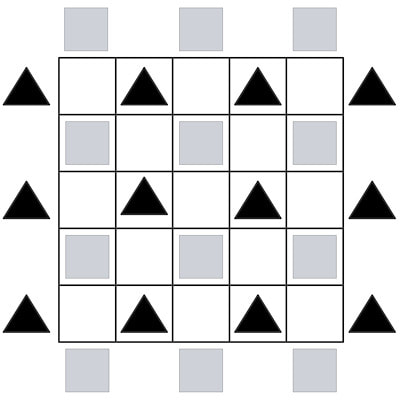
In Diagram 3, visualize the 25 cells inside the square as 1x1x1 cubes, which form the horizontal bottom, middle, and top Layers of the 5x5x5 Qua Cube Game Board shown in Diagram 1. Diagrams 4 and 5 are two more Bridg-It Square game board representations of Diagram 2. The 25 cells inside the 5x5 squares in these figures can also be visualized as 1x1x1 cubes. Diagram 4 forms the front, middle and back vertical Ranks of Diagram 1. Diagram 5 forms the left, middle and right vertical Files of Diagram 1.
Using the terminology Layers, Ranks and Files will help describe 3D orientations when forming the Qua Cube game board extension to the Bridg-It Square game board.
In Diagram 3, visualize the 25 cells inside the square as 1x1x1 cubes, which form the horizontal bottom, middle, and top Layers of the 5x5x5 Qua Cube Game Board shown in Diagram 1. Diagrams 4 and 5 are two more Bridg-It Square game board representations of Diagram 2. The 25 cells inside the 5x5 squares in these figures can also be visualized as 1x1x1 cubes. Diagram 4 forms the front, middle and back vertical Ranks of Diagram 1. Diagram 5 forms the left, middle and right vertical Files of Diagram 1.
Inside the 5x5x5 Qua Cube Game Board shown in Diagram 1, there are four cells in each of the even numbered planes (Layers, Ranks and Files) that correspond to the locations above and below the four parallel bridge placement locations in Diagram 2. To maintain 3D rotational symmetry, they could not be filled in with any of the three qua identifying marks. They could have been specified as null cells, unavailable for game play. However, to guarantee there is always a winner for a 5x5x5 Qua game, it is necessary for these cells (eight total) to be empty and available for game play when two adjacent cells are occupied by the same qua.
Proving there is always a winner for Qua Games where N is odd is a challenge to the reader. Another challenge is constructing an alternate initial Qua Cube game board layout where N = 4 that avoids frequent draws or a forced win by the first player. An example is given in Qua (Pidcock, 2019).
Proving there is always a winner for Qua Games where N is odd is a challenge to the reader. Another challenge is constructing an alternate initial Qua Cube game board layout where N = 4 that avoids frequent draws or a forced win by the first player. An example is given in Qua (Pidcock, 2019).
Sherwood Pidcock, who goes by Woody, currently lives in Washington State. Woody is a lifelong student and teacher who loves mathematics, especially geometry. Martha is Woody's daughter.
Qua is a most unusual three-dimensional game. As I mentioned in the description of 3D XYZ Chess, genuinely three-dimensional games are a rarity, perhaps with two exceptions, three-dimensional alignment games and three-dimensional chess games. Qua is the first three-dimensional connection game, at least in my experience. But somehow, it makes complete logical sense—there are three pairs of opposite faces on a cube, each pair to be connected by one of the three players. Just as Qua is a translation of Bridg-It into a third dimension, are there any other square-based connection games that can likewise be extended to three-player games? How about Slither? ~ Ed.
Qua is a most unusual three-dimensional game. As I mentioned in the description of 3D XYZ Chess, genuinely three-dimensional games are a rarity, perhaps with two exceptions, three-dimensional alignment games and three-dimensional chess games. Qua is the first three-dimensional connection game, at least in my experience. But somehow, it makes complete logical sense—there are three pairs of opposite faces on a cube, each pair to be connected by one of the three players. Just as Qua is a translation of Bridg-It into a third dimension, are there any other square-based connection games that can likewise be extended to three-player games? How about Slither? ~ Ed.