Hexagonal Go
Algae bloom, San Francisco Bay, aerial view.*
|
by Thibault Pillon
|
Blooms is Nick Bentley’s take on Hexagonal Go. Nick claims it solves the problems arising when Go is ported directly to a hexagonal tessellation. Before we find out if that is true, let us recall the main issue with Hexagonal Go.
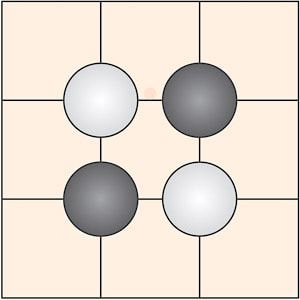
Hexagonal Go’s most obvious problem is that each cell has six neighbouring cells instead of four. In a game where you catch opponent stones by reducing their liberties, the hunted quickly outruns the hunter. Cross-cuts are another key aspect of Go:
Hexagonal Go’s most obvious problem is that each cell has six neighbouring cells instead of four. In a game where you catch opponent stones by reducing their liberties, the hunted quickly outruns the hunter. Cross-cuts are another key aspect of Go:
Figure 1: A cross-cut in Go.
A cross-cut is a meeting point, where both players end up with two disconnected groups. In Go, cross-cuts are aggressive play, usually provoking big fights, since losing a cross-cut stone effectively allows your opponent to connect her two groups on opposite sides of the cross-cut, giving her a big advantage.
But cross-cuts do not exist on hexagonal tessellations. To see why, observe that playing on the cells of a hexagonal lattice is equivalent to playing on the vertices of a triangular lattice. In classical Go, cross-cuts are formed around a cell of the square lattice where each diagonal is occupied by stones of a given colour. On the other hand, a triangle cell with all three vertices occupied always contains a pair of stones of the same colour. This means the stones do not mutually disconnect each other. It is for this very reason, by way, that Hex cannot end in a draw. When you play Go on a hexagonal board, the extra liberties and lack of crosscuts limit your attacking options, which makes the game dull.
How to fix this? Let us focus on two ideas: Keil and Trigo. Keil was deeply covered in AG18. It deals with the board’s high connectivity by restricting the notion of connectedness in a strange, yet clever, way. The upside is it does so effectively and recreates cross-cuts. The downside is it feels unnatural. In addition, you can argue that, though Keil is played on a hexagonal board, the game’s underlying topology is not a hexagonal tessellation, but a strange network of points and edges influenced by the game state.
Trigo is simply Hexagonal Go with a 12* rule. (See David Ploog's discussion of movement protocols in AG19.) Except for the first player’s first turn, each player can play two stones on each turn. This balances the advantage of playing first, since each player ends her own turn having played one more stone than her opponent. (In a normal game of Go, this is dealt with using komi, which grants a few extra points for the second player.) More to the point, it is also an attempt to deal with the board’s high connectivity. Groups with few liberties are more at risk, groups now need three eyes to live, and solid shapes like bridges are no longer unconditionally connected. However, the additional attacking power is counter-balanced by additional defensive power: you get two consecutive plays to get out of tricky situations.
Blooms follows the second idea with a twist. It is Go, on a hexagonal board, with a 12* rule, where each player controls two different colours. After the first player’s first turn, each player places one stone of each of her colours on every turn. A player may also place only one stone per turn if she wishes, which will mostly happen at the game’s end, when playing stones in your own territory hurts you.
The key point of this rule, which will baffle the Go player at first, is that a group is surrounded, and thus captured, when all its liberties are occupied by differently coloured stones, even if they are friendly. In other words, you can and will take your own liberties when playing.
Now I will discuss Blooms in greater depth. First, I will illustrate how Blooms overcomes the extra liberties and lack of cross-cuts on hexagonal boards. Second, I will point out some features Blooms and Go share in common, like cyclical repeating positions. Third, I will point out two interesting features of Blooms that distinguish it from Go: the high prevalence of sacrifice plays, and the concept of the "Big Eye."
Let us start with Blooms’ rules, taken from Nick Bentley's website, with modified terminology to align more closely with that of Go:
But cross-cuts do not exist on hexagonal tessellations. To see why, observe that playing on the cells of a hexagonal lattice is equivalent to playing on the vertices of a triangular lattice. In classical Go, cross-cuts are formed around a cell of the square lattice where each diagonal is occupied by stones of a given colour. On the other hand, a triangle cell with all three vertices occupied always contains a pair of stones of the same colour. This means the stones do not mutually disconnect each other. It is for this very reason, by way, that Hex cannot end in a draw. When you play Go on a hexagonal board, the extra liberties and lack of crosscuts limit your attacking options, which makes the game dull.
How to fix this? Let us focus on two ideas: Keil and Trigo. Keil was deeply covered in AG18. It deals with the board’s high connectivity by restricting the notion of connectedness in a strange, yet clever, way. The upside is it does so effectively and recreates cross-cuts. The downside is it feels unnatural. In addition, you can argue that, though Keil is played on a hexagonal board, the game’s underlying topology is not a hexagonal tessellation, but a strange network of points and edges influenced by the game state.
Trigo is simply Hexagonal Go with a 12* rule. (See David Ploog's discussion of movement protocols in AG19.) Except for the first player’s first turn, each player can play two stones on each turn. This balances the advantage of playing first, since each player ends her own turn having played one more stone than her opponent. (In a normal game of Go, this is dealt with using komi, which grants a few extra points for the second player.) More to the point, it is also an attempt to deal with the board’s high connectivity. Groups with few liberties are more at risk, groups now need three eyes to live, and solid shapes like bridges are no longer unconditionally connected. However, the additional attacking power is counter-balanced by additional defensive power: you get two consecutive plays to get out of tricky situations.
Blooms follows the second idea with a twist. It is Go, on a hexagonal board, with a 12* rule, where each player controls two different colours. After the first player’s first turn, each player places one stone of each of her colours on every turn. A player may also place only one stone per turn if she wishes, which will mostly happen at the game’s end, when playing stones in your own territory hurts you.
The key point of this rule, which will baffle the Go player at first, is that a group is surrounded, and thus captured, when all its liberties are occupied by differently coloured stones, even if they are friendly. In other words, you can and will take your own liberties when playing.
Now I will discuss Blooms in greater depth. First, I will illustrate how Blooms overcomes the extra liberties and lack of cross-cuts on hexagonal boards. Second, I will point out some features Blooms and Go share in common, like cyclical repeating positions. Third, I will point out two interesting features of Blooms that distinguish it from Go: the high prevalence of sacrifice plays, and the concept of the "Big Eye."
Let us start with Blooms’ rules, taken from Nick Bentley's website, with modified terminology to align more closely with that of Go:
Rules
- Blooms is played on the spaces of a base 4, 5, or 6 hexhex board. Larger sizes, too, are playable. Player 1 uses Red and Yellow stones; Player 2 uses Blue and Black stones.
- Player 1 places a Red or Yellow stone on an empty space. Then Player 2 places one or two stones of her colour on one or two empty spaces, and if Player 2 places two stones they must be of different colours.
- Thereafter, the players alternate turns, placing one or two stones of their colour on empty spaces, with the proviso that two stones placed must be of different colours.
- A group is a connected set of stones of a single colour; a group has liberties if it has adjacent empty spaces.
- After placing one or two stones, a player captures all enemy groups with no liberties by removing them from the board.
- The first player to capture a pre-determined number of enemy stones wins the game. The author recommends 15 for a base 4 and 20 for a base 5. For larger sizes, players may experiment, with 25 or 30, say, with base 6.
Liberties
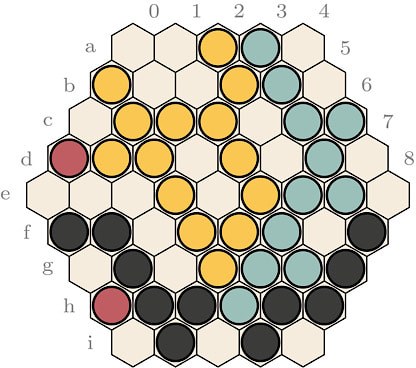
Blooms effectively solves the hex board’s high connectivity problem. Groups are often in danger of being captured, or simply are captured. The game’s four-colour nature allows your opponent to attack a group using both of her colours, while you can only extend your liberties with a single move of the attacked colour. Blooms at a high level of play (or what is currently the highest standard of play) has a lot of liberty fights and close races.
Cross-cuts
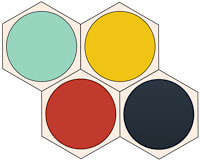
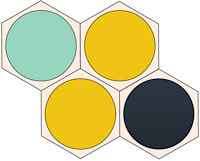
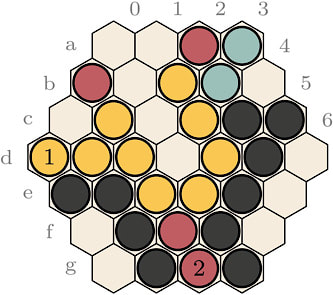
Blooms has something similar to cross-cuts, but with a twist. Though each triangle cell has at least two adjacent friendly stones when filled, these can be of different colours, creating two friendly groups that nonetheless block each other and reduce each other’s liberties. What would be a cross-cut in Keil can now be a meeting of four groups of different colours, as in Figure 2, below. But there’s an imbalance in this situation: one player has his two friendly colours connected to each other. So, for example, if Red and Yellow are connected through a cross-cut, the loss of one of the group (e.g. Red) will allow for the other group (hence Yellow) to dive into the created void, as in Figure 3, below. But if the Blue or Black group is captured, Blue-Black cannot benefit in the same way.
Blooms effectively solves the hex board’s high connectivity problem. Groups are often in danger of being captured, or simply are captured. The game’s four-colour nature allows your opponent to attack a group using both of her colours, while you can only extend your liberties with a single move of the attacked colour. Blooms at a high level of play (or what is currently the highest standard of play) has a lot of liberty fights and close races.
Cross-cuts
Blooms has something similar to cross-cuts, but with a twist. Though each triangle cell has at least two adjacent friendly stones when filled, these can be of different colours, creating two friendly groups that nonetheless block each other and reduce each other’s liberties. What would be a cross-cut in Keil can now be a meeting of four groups of different colours, as in Figure 2, below. But there’s an imbalance in this situation: one player has his two friendly colours connected to each other. So, for example, if Red and Yellow are connected through a cross-cut, the loss of one of the group (e.g. Red) will allow for the other group (hence Yellow) to dive into the created void, as in Figure 3, below. But if the Blue or Black group is captured, Blue-Black cannot benefit in the same way.
Figure 2: A Keil-type crosscut.
|
Figure 3: With the Red stone captured, a Yellow stone can jump in to connect.
|
Go concepts
A lot of Go concepts translate to Blooms. For example:
Cyclical positions
Blooms lacks Go’s short repeating cycles (called ko). But it has longer cycles and the rules address them in an interesting way. There are two obvious ways to deal with long cycles: a super-ko rule, which forbids the same situation from happening twice, or allow the game to end in a draw. Blooms takes a third way: it sets a certain number of captures as the unique winning condition of the game. Interestingly, the game often ends in the board being shared as it would be in a normal game of Go. In this situation, instead of passing, players simply fill their territory until they are forced to give each other prisoners by playing in the opponent's area. Note that at this stage, it is not profitable anymore to play two stones every turn, which is the reason for allowing players to play a single stone on their turn.
Blooms’ inventor claims this winning condition emulates area scoring with a group tax. That is roughly correct, but not always. It works under the assumption that both players have played the same number of stones, but there are situations when a player is forced to answer a threat from a single stone by playing two stones. Or someone might want to launch an attack by playing two stones several times, when the opponent responds with only one stone each time. These imbalances are not indicative of perfect play, but they show that in actual play, things might get a little bit trickier than counting areas.
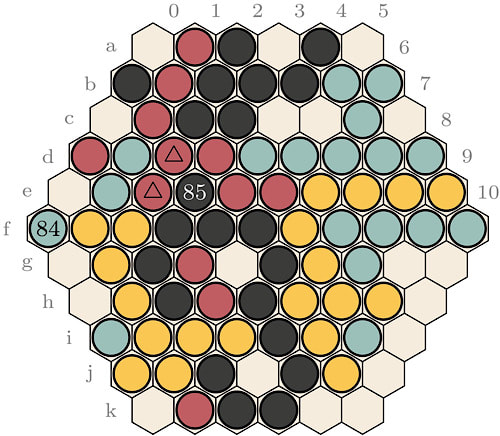
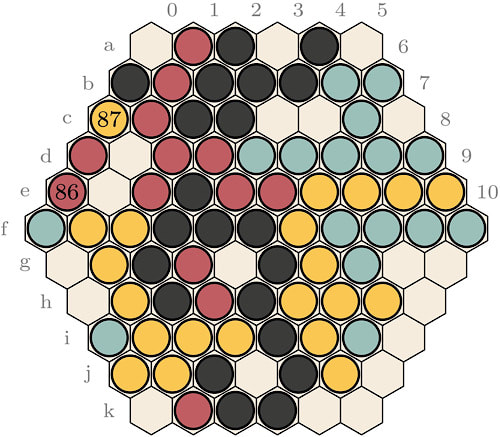
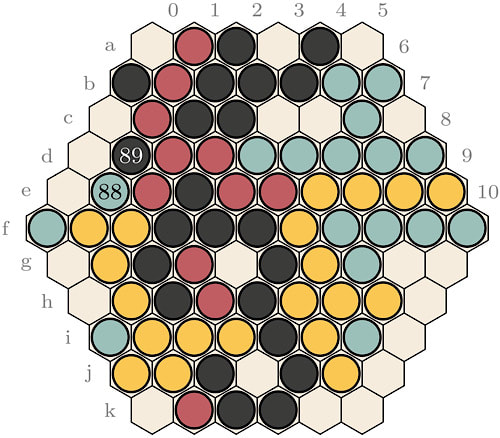
I have personally seen only one cycle occur in one of my games. This cycle is depicted in Figures 4, 5, and 6.
A lot of Go concepts translate to Blooms. For example:
- Liberties and liberty races, as already mentioned.
- Blooms has the notion of eyes. A group surrounded by enemy stones must create three eyes to live.
- Blooms has a very interesting family of seki-like situations. Enemy groups can share a single eye of three liberties, they can each have a proper liberty and share an eye of two liberties (or two of one for that matter) or each have two proper eyes and a shared one. But this is not limited to groups of enemy stones. Sharing eyes also is a powerful way of giving life to several (usually two) groups of your own.
Cyclical positions
Blooms lacks Go’s short repeating cycles (called ko). But it has longer cycles and the rules address them in an interesting way. There are two obvious ways to deal with long cycles: a super-ko rule, which forbids the same situation from happening twice, or allow the game to end in a draw. Blooms takes a third way: it sets a certain number of captures as the unique winning condition of the game. Interestingly, the game often ends in the board being shared as it would be in a normal game of Go. In this situation, instead of passing, players simply fill their territory until they are forced to give each other prisoners by playing in the opponent's area. Note that at this stage, it is not profitable anymore to play two stones every turn, which is the reason for allowing players to play a single stone on their turn.
Blooms’ inventor claims this winning condition emulates area scoring with a group tax. That is roughly correct, but not always. It works under the assumption that both players have played the same number of stones, but there are situations when a player is forced to answer a threat from a single stone by playing two stones. Or someone might want to launch an attack by playing two stones several times, when the opponent responds with only one stone each time. These imbalances are not indicative of perfect play, but they show that in actual play, things might get a little bit trickier than counting areas.
I have personally seen only one cycle occur in one of my games. This cycle is depicted in Figures 4, 5, and 6.
Figure 4: Desperis (RY) - Gulchen (UB).
 Figure 5: Continuation from Fig. 4.
|
Figure 6: Continuation from Fig. 5.
|
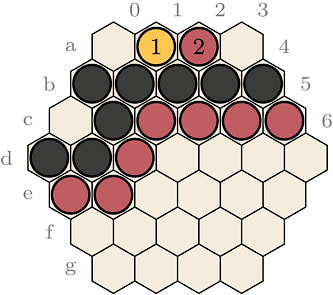
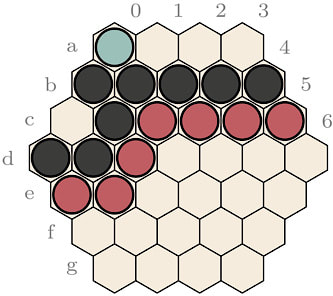
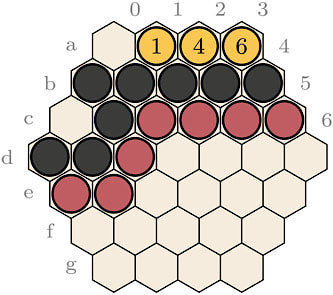
Observe that the top red group in Figure 4 is in immediate threat of being captured, Red-Yellow has no other option, throughout the cycle but to defend this group. Also observe that the Black bottom group has only three liberties and no way to escape. The sequence depicted in the diagram is thus forced for both players, since a capture of either group (Red or Black) would be a definite loss. The outcome of this cycle depends on the number of captures of both players. This game was played with a 30 limit. It is interesting to note that Red-Yellow can break the cycle at any time to capture the five blue stones on the right. Blue-Black, also, can use a move to capture the three Red stones on the bottom. This cycle hence comes down to whether Red-Yellow will cross the 25 prisoners line before Blue-Black crosses the 27 prisoners line.
Sacrifice play
A big aspect of Blooms is it allows for many sacrifice plays. And I mean a lot! Here is why: players are allowed to place stones on any empty cells, including cells that render one of their own groups surrounded. After placing the stones, a player removes any surrounded groups of enemy stones, but not her own. Stones which "committed suicide" this turn remain on the board until the end of the opponent’s turn. This allows for many beautiful strategies.
Figure 7 shows how it is possible to sacrifice stones to cut an opponent's group. When playing 2 in this diagram Red-Yellow is sacrificing two stones which will be removed only before his next turn. If he commits to this strategy, he can follow it by (Yf4,Rg5) once again sacrificing a stone to maintain the cut. On his next turn, he plays (?,Yg5) for the finishing blow. Similarly, observe that Blue-Black cannot breach the yellow territory by capturing a2. Red-Yellow would simply replace the red captured stone by a yellow stone to seal his territory. Finally, for the same reason b4 and c0 are real eyes for the black group and yellow group, respectively.
Sacrifice play
A big aspect of Blooms is it allows for many sacrifice plays. And I mean a lot! Here is why: players are allowed to place stones on any empty cells, including cells that render one of their own groups surrounded. After placing the stones, a player removes any surrounded groups of enemy stones, but not her own. Stones which "committed suicide" this turn remain on the board until the end of the opponent’s turn. This allows for many beautiful strategies.
Figure 7 shows how it is possible to sacrifice stones to cut an opponent's group. When playing 2 in this diagram Red-Yellow is sacrificing two stones which will be removed only before his next turn. If he commits to this strategy, he can follow it by (Yf4,Rg5) once again sacrificing a stone to maintain the cut. On his next turn, he plays (?,Yg5) for the finishing blow. Similarly, observe that Blue-Black cannot breach the yellow territory by capturing a2. Red-Yellow would simply replace the red captured stone by a yellow stone to seal his territory. Finally, for the same reason b4 and c0 are real eyes for the black group and yellow group, respectively.
Figure 7: The black group is cut.
Figure 8 shows an extreme example of a sacrifice play. It is the Red-Yellow turn and, assuming he can sacrifice enough stones, he has a strategy to capture the left black stones. By playing Ri6 at every turn while slowly filling the group’s outside liberties, Red-Yellow effectively prevents Blue-Black connecting to the right black group. In the discussion of the Big Eye, we will see Red-Yellow can fill the inside liberties of the black group without getting stuck in a loop. Figure 8 also shows an interesting example of a shared life between the right black and blue groups.
Figure 8: The left black group will be captured.
The Big Eye
Figure 9 and the succeeding figures show an interesting phenomenon that I like to call the "Big Eye."
Figure 9 and the succeeding figures show an interesting phenomenon that I like to call the "Big Eye."
Figure 9: Black is alive with a Big Eye.
Figure 11: Continuation of Fig. 10.
|
Figure 10: Continuation of Fig. 9.
Figure 12: Continuation of Fig. 11.
|
Black already secured an eye at c0 and has another made of a line of four cells. It is tempting for Red-Yellow to play as shown in Figure 9 to block black from making three eyes. Next, if Red-Yellow wants to attack the black group, he has to attack her liberties from the inside. First (Ra3, pass) sacrificing two red stones, Blue-Black does not need to answer, then (pass, Ya2), then (pass,Ya3) which leads to Figure 10. Now, if Blue-Black were to capture with a black stone, she would critically reduce her own liberties and the group would be doomed. I think this would be the first instinct of every Go player. The key play here is to capture with a blue stone as shown in Figure 11. Black is now threatening to play either a1 or a2 to form second and third eyes, but if Red-Yellow now plays both of these points, it simply reverts to Figure 9. If Red-Yellow plays a single stone at a1, he captures the blue stone and Blue-Black can freely take a2. The last possible strategy for Red-Yellow is to play a single stone at a2 and Blue-Black should refrain herself from playing a1 as this would not remove the a0 blue stone and Red-Yellow would simply capture everything on the next turn. Blue-Black simply passes and the only remaining play for Red-Yellow is a3, which does not work, as shown in Figure 12. This situation happens quite a lot in actual play and I like to think about it with the proverb, ”A Big Eye is worth two eyes.”
There is much more to investigate about Blooms, which is a deep and interesting game. I recommend it as a colourful, workable, and deep Hexagonal Go.
There is much more to investigate about Blooms, which is a deep and interesting game. I recommend it as a colourful, workable, and deep Hexagonal Go.
Blooms is a game by Nick Bentley, who is one of the very active modern abstract game designers producing highly original new games. His first big hit was Catchup, which was implemented on Little Golem in 2010. Catchup has attracted a consistent following, with regular tournaments and a number of very strong players. Several other of Nick's games, including Circle of Life and its successor Bug have attracted much attention, and Circle of Life, as well as Blooms, is playable on BoardGameArena.
Thibault has admirably pointed out some key features of Blooms that demonstrate how interesting and original it is. To my mind the tactics around sacrificing stones are particularly deserving of attention, although I suspect there is much more that Thibault did not touch on at this time. The sacrifice tactics emerge from the rule that only opponent's dead groups are removed at the end of your turn, a rule which obviously is a brilliant design decision. It is wonderful when strategy and tactics unfold in this manner from seemingly unrelated rules.
One of the things I wondered about when I first learned of Blooms was its scalability. Go, for example, scales seamlessly from 9x9 up to 19x19, and beyond. The grand strategies of Go only become apparent in the larger sizes. The largest size of board on which Blooms is played regularly seems to be the base-6 board used, for example, on BoardGameArena, with 91 spaces. How would Blooms work on a base-10 or base-11 board, for example, taking it closer to the scale of a 19x19 Go board? I asked this question of Thibault, who answered as follows:
"The current available sizes on BoardGameArena, base 4, base 5, and base 6 already show that the size impacts the game play. While base 4 is really a toy model of the game, base 5 feels similar to playing Go on a 9x9 board. On a base-5 board, there is no place for more than one group of each colour. Usually, games which do not end by resignation or annihilation of one player's stones, will end in the board being split in exactly two areas between Red-Yellow and Blue-Black. This can often be one Red group and one Yellow group sharing life or simply one group of a single colour, all stones of the friendly colour having been wiped off of the board as cannon fodder. Base 6 already has a slower pace which feels closer to a 13x13 Go board. I would be very interested in playing Blooms on a base-9 board, with at least a 50 prisoners limit to see how the game scales up. Is local stability eventually achieved, in the sense that the game progresses from one local fight to another or do 'all or nothing' situations predominate? It is certainly a topic that needs to be explored. With a larger board, Blooms might very well see tactical and strategic emerging complexity comparable with that of Go and Hex, for example."
Blooms' designer, Nick Bentley, added,
"I've kept the game limited to small sizes to start not because I think it's best on those sizes, but because everyone's a beginner and people learn best on small boards before scaling up. That seems especially important for Blooms, because of its many tactics, like the scope for sacrifice play mentioned in the article. In my experience, new players, even many players familiar with Go, often fail to see much of what's going on at a tactical level at first, and I want to figure out how to improve that situation. For experienced players, I believe the best version of the game will likely be on larger boards than are available now, but not as large as 19x19 Go. If I had to guess, I'd guess a board with somewhere around 200 to 250 cells will be best for competitive play. But that assumes the game will have local stabilities on the larger boards. My intuition suggests it will, but we'll see."
Lastly, Nick made the following comment to further address Thibault’s point in the article that Keil seems unnatural:
"In Keil, you can have two friendly stones that are visually connected, but which are functionally disconnected for the purpose of gameplay. This mismatch between visuals and game state is incredibly hard on the brain, which is designed to see regions of contiguous colour in the visual field as unified things (see my article on perceptual binding). So Keil forces you to "unlearn" a basic, evolutionarily-programmed assumption our brains automatically make. That's why it feels so weird. This demands a large amount of cognitive overhead, which will in turn make it hard for anyone to see deeply into the game."
The perceptual issues in Keil are a good point, and perhaps Keil does require a new way of thinking. However, the approach of Keil can be thought of as natural to the hexagonal tessellation, as I pointed out after the Keil article in AG18. Simply put, the smallest connected unit in Keil is an equilateral triangle of adjacent stones, rather than the pair of stones of Go—a new slant on the concept of connectivity. I have to admit that Keil does require a game or two to get familiar with a few key shapes. Thereafter, Keil positions ought to be no more difficult to read than Go positions of corresponding complexity. I might add finally that Bloom’s four colours versus two entails its own perceptual challenges, although again easy to get used to. Either way, Blooms offers an admirable counterpoint to Keil. Both games are highly original and successful solutions to the problems that emerge when trying to play Go on a hexagonal tessellation. Both games have interesting tactics that are not present in Go itself. ~ Ed.
Thibault has admirably pointed out some key features of Blooms that demonstrate how interesting and original it is. To my mind the tactics around sacrificing stones are particularly deserving of attention, although I suspect there is much more that Thibault did not touch on at this time. The sacrifice tactics emerge from the rule that only opponent's dead groups are removed at the end of your turn, a rule which obviously is a brilliant design decision. It is wonderful when strategy and tactics unfold in this manner from seemingly unrelated rules.
One of the things I wondered about when I first learned of Blooms was its scalability. Go, for example, scales seamlessly from 9x9 up to 19x19, and beyond. The grand strategies of Go only become apparent in the larger sizes. The largest size of board on which Blooms is played regularly seems to be the base-6 board used, for example, on BoardGameArena, with 91 spaces. How would Blooms work on a base-10 or base-11 board, for example, taking it closer to the scale of a 19x19 Go board? I asked this question of Thibault, who answered as follows:
"The current available sizes on BoardGameArena, base 4, base 5, and base 6 already show that the size impacts the game play. While base 4 is really a toy model of the game, base 5 feels similar to playing Go on a 9x9 board. On a base-5 board, there is no place for more than one group of each colour. Usually, games which do not end by resignation or annihilation of one player's stones, will end in the board being split in exactly two areas between Red-Yellow and Blue-Black. This can often be one Red group and one Yellow group sharing life or simply one group of a single colour, all stones of the friendly colour having been wiped off of the board as cannon fodder. Base 6 already has a slower pace which feels closer to a 13x13 Go board. I would be very interested in playing Blooms on a base-9 board, with at least a 50 prisoners limit to see how the game scales up. Is local stability eventually achieved, in the sense that the game progresses from one local fight to another or do 'all or nothing' situations predominate? It is certainly a topic that needs to be explored. With a larger board, Blooms might very well see tactical and strategic emerging complexity comparable with that of Go and Hex, for example."
Blooms' designer, Nick Bentley, added,
"I've kept the game limited to small sizes to start not because I think it's best on those sizes, but because everyone's a beginner and people learn best on small boards before scaling up. That seems especially important for Blooms, because of its many tactics, like the scope for sacrifice play mentioned in the article. In my experience, new players, even many players familiar with Go, often fail to see much of what's going on at a tactical level at first, and I want to figure out how to improve that situation. For experienced players, I believe the best version of the game will likely be on larger boards than are available now, but not as large as 19x19 Go. If I had to guess, I'd guess a board with somewhere around 200 to 250 cells will be best for competitive play. But that assumes the game will have local stabilities on the larger boards. My intuition suggests it will, but we'll see."
Lastly, Nick made the following comment to further address Thibault’s point in the article that Keil seems unnatural:
"In Keil, you can have two friendly stones that are visually connected, but which are functionally disconnected for the purpose of gameplay. This mismatch between visuals and game state is incredibly hard on the brain, which is designed to see regions of contiguous colour in the visual field as unified things (see my article on perceptual binding). So Keil forces you to "unlearn" a basic, evolutionarily-programmed assumption our brains automatically make. That's why it feels so weird. This demands a large amount of cognitive overhead, which will in turn make it hard for anyone to see deeply into the game."
The perceptual issues in Keil are a good point, and perhaps Keil does require a new way of thinking. However, the approach of Keil can be thought of as natural to the hexagonal tessellation, as I pointed out after the Keil article in AG18. Simply put, the smallest connected unit in Keil is an equilateral triangle of adjacent stones, rather than the pair of stones of Go—a new slant on the concept of connectivity. I have to admit that Keil does require a game or two to get familiar with a few key shapes. Thereafter, Keil positions ought to be no more difficult to read than Go positions of corresponding complexity. I might add finally that Bloom’s four colours versus two entails its own perceptual challenges, although again easy to get used to. Either way, Blooms offers an admirable counterpoint to Keil. Both games are highly original and successful solutions to the problems that emerge when trying to play Go on a hexagonal tessellation. Both games have interesting tactics that are not present in Go itself. ~ Ed.
Header image
* Salt evaporation ponds formed by salt water impounded within levees in former tidelands on the shores of San Francisco Bay. Doc Searls from Santa Barbara, USA, CC BY 2.0 <https://creativecommons.org/licenses/by/2.0>, via Wikimedia Commons.
* Salt evaporation ponds formed by salt water impounded within levees in former tidelands on the shores of San Francisco Bay. Doc Searls from Santa Barbara, USA, CC BY 2.0 <https://creativecommons.org/licenses/by/2.0>, via Wikimedia Commons.